Bipartite Matching and Hungarian Algorithm

引言

二分图匹配和匈牙利算法（Bipartite Matching and Hungarian Algorithm）在CV领域的后处理算法中是经常可以看到的，比如以下的一些论文：

2017年的CVPR工作，OpenPose 利用bipartite matching 来进行，同关节类型的多个人体关键点分配到不同的隶属人体
2020年的End-to-end Object Detection with Transformer直接构造了一个Hungarian Loss，来解决预测目标与真实目标的分配问题
2020年CVPR Compressed Volumetric Heatmaps for Multi-Person 3D Pose Estimation中多人人体3D距离匹配算法
多目标跟踪领域内的，前后相邻帧匹配问题
在Instance Segmentation领域，这也是很常见的

顾名思义，二分图匹配是一个分配问题 (Assignment Problem)。

Hungarian Algorithm (匈牙利算法) 是在1955年提出的¹ .

如果想要彻底理解它，需要先掌握它所涉及到的一些概念，作为先验知识。如下所示：

图
边与节点
增广路
匹配
最大匹配
完美匹配
二分图
匈牙利算法
KM算法
BFS搜索与队列思想解决迷宫最短路径问题

二分图的最大匹配

名词解释

首先将我们遇到的问题转换成分配问题。我们的数据以一种二分图的数据结构呈现。

什么是二分图呢，它是一种特殊的图，即可以将图分为两组，两组内的节点之间没有连接边，两组之间节点存在连接关系。

我们的目标是寻找一个最大的匹配结果，使得匹配结果最合理。

比如说，我们想在一群男生和一群女生之间，根据他们各自喜欢的异性，找到一种能够成全更多对情侣的方案。又比如说，我们打算把工作项目，指派给员工们，希望用一种最大效率或者最低成本的方案。

最大匹配，即，在任意一个节点最多只有一个边与之相连接的条件下，尽可能使得两组之间的匹配边数最多。这就是我们的最优匹配目标，那么，如何求解出一种匹配方式，能够达到最大匹配呢？

最粗暴的算法就是暴力搜索，然而它的时间复杂度是指数级O(n!)

那有没有可以降低复杂度，并能够确定找到最优解的算法呢？

有，匈牙利算法就是！

匈牙利算法是一个什么算法呢？一种搜索算法，怎么样去搜索解呢？

其中，引入一种增广路的概念，它能在暴力搜索的过程中能够用一种简单的策略来改进当前匹配结果，直到我们无法找到更优的匹配。

增广路是什么意思呢，就是一种特殊的交错路，它从一个未匹配点出发，经过未匹配边、已匹配边、未匹配边,...,直到到达另外一个未匹配点，那么这样交换交错路径（匹配边和未匹配边），就总能改进匹配，因为增广路上的未匹配边总比匹配边多1个，交换就意味着改进，因为我们想要最多的匹配边。

术语理解

基本概念讲完了。求解最大匹配问题的一个算法是匈牙利算法，下面讲的概念都为这个算法服务。

Fig 5

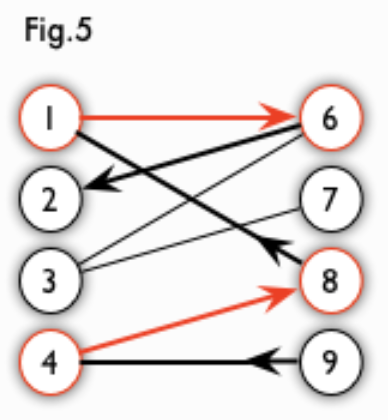
交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。

增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路（agumenting path）。例如，图 5 中的一条增广路如图 6 所示（图中的匹配点均用红色标出）：

Fig6

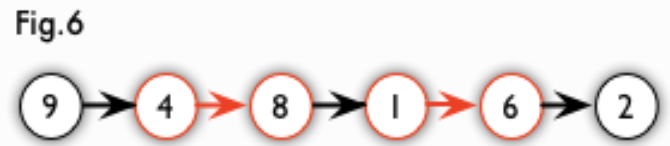
增广路有一个重要特点：非匹配边比匹配边多一条。因此，研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边，所以这样做不会破坏匹配的性质。交换后，图中的匹配边数目比原来多了 1 条。

我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时，达到最大匹配（这是增广路定理）。匈牙利算法正是这么做的。在给出匈牙利算法 DFS 和 BFS 版本的代码之前，先讲一下匈牙利树。

匈牙利树一般由 BFS 构造（类似于 BFS 树）。从一个未匹配点出发运行 BFS（唯一的限制是，必须走交替路），直到不能再扩展为止。例如，由图 7，可以得到如图 8 的一棵 BFS 树：

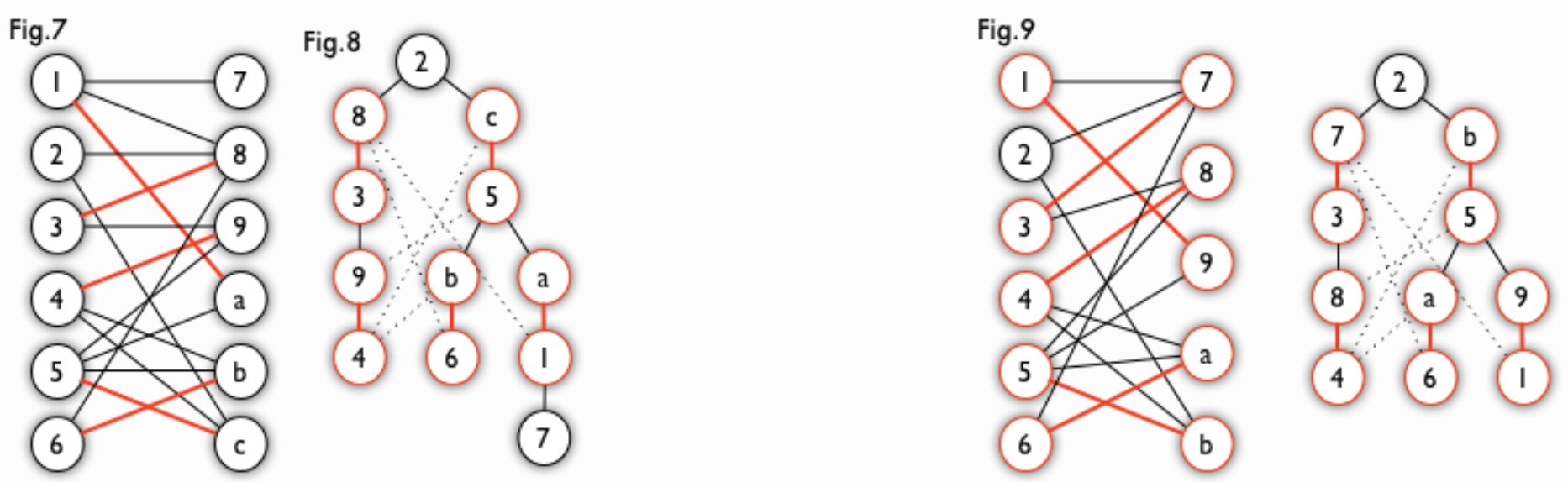
这棵树存在一个叶子节点为非匹配点（7 号），但是匈牙利树要求所有叶子节点均为匹配点，因此这不是一棵匈牙利树。如果原图中根本不含 7 号节点，那么从 2 号节点出发就会得到一棵匈牙利树。这种情况如图 9 所示（顺便说一句，图 8 中根节点 2 到非匹配叶子节点 7 显然是一条增广路，沿这条增广路扩充后将得到一个完美匹配）。

Kuhn-Munkres算法(二分图最大权匹配)

在进入加权二分图之前，我们默认已经掌握了图、交错路径、增广路径、最大匹配和完美匹配的概念

上面探讨的二分图匹配问题中，任意两个节点之间，要么是有边的，要么是没有边。在很多情况下，节点之间的候选连接是有强度的，带权值的。

在这种情况下，整体最优的匹配是，我们希望找到一种方案（依然是一点至多只有一个边的条件）使得我们的成本最少或者权重和最大。

原理

Kuhn-Munkres 算法的原理是什么呢？

先一言以蔽之

The KM theorem transforms the problem from an op- timization problem of finding a max-weight matching into a combinatorial one of finding a perfect match- ing. It combinatorializes the weights. This is a classic technique in combinatorial optimization. KM定理将问题从寻找最大权重匹配的优化问题转变为寻找完美匹配的组合问题。它组合了权重。这是组合优化中的经典技术。

如何转换的呢？

KM又引入了Feasible Labelings& Equality Graphs这两个概念

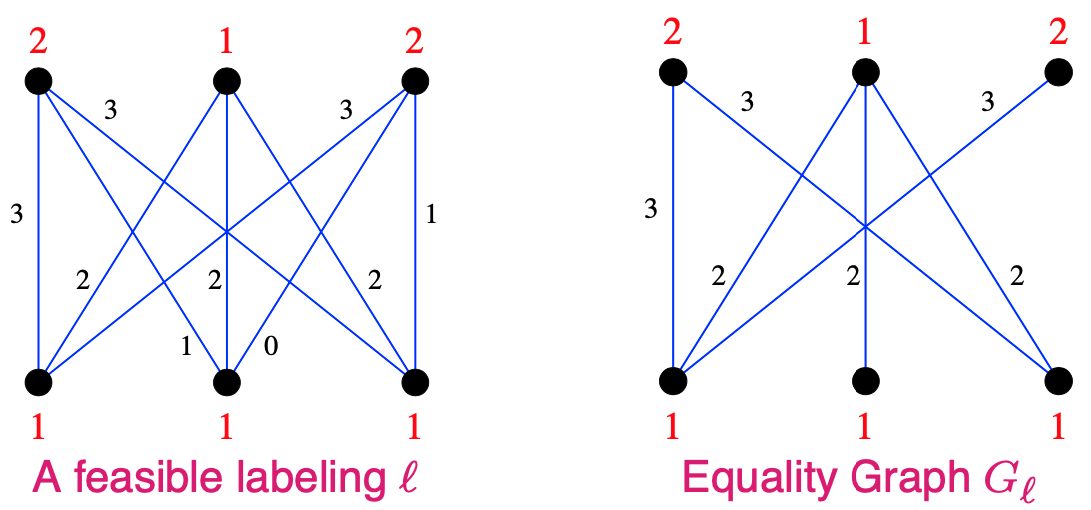
Feasible Labelings & Equality Graphs

A vetex labeling is a function $\ell: V \rightarrow \mathcal{R}$
A feasible labeling is one such that \[ \ell(x)+\ell(y) \geq w(x, y), \quad \forall x \in X, y \in Y \]
the Equality Graph (with respect to $\ell$) is $G=\left(V, E_{\ell}\right)$ where \[ E_{\ell}=\{(x, y): \ell(x)+\ell(y)=w(x, y)\} \]

理论与证明

Theorem[Kuhn-Munkres]: If $\ell$ is feasible and $M$ is a Perfect matching in $E_{\ell}$ then $M$ is a max-weight matching.

如果能找到一个取值节点策略 $\ell: V \rightarrow \mathcal{R}$ ，使得满足Feasible Labelings & Equality Graphs 两个条件，就可以找到最大匹配

The KM theorem transforms the problem from an optimization problem of finding a max-weight matching into a combinatorial one of finding a perfect matching. It combinatorializes the weights. This is a classic technique in combinatorial optimization.

Notice that the proof of the KM theorem says that for any matching $M$ and any feasible labeling $\ell$ we have \[ w(M) \leq \sum_{v \in V} \ell(v) \] This has very strong echos of the max-flow min-cut theorem.

Proof:

只要证明：任意一个匹配解的权重和的上界都不大于 $\sum_{v \in V} \ell(v)$

Denote edge $e \in E$ by $e=\left(e_{x}, e_{y}\right)$ Let $M^{\prime}$ be any PM in $G$ (not necessarily in in $E_{\ell}$ ). since every $v \in \bar{V}$ is covered exactly once by $M$ we have \[ w\left(M^{\prime}\right)=\sum_{e \in M^{\prime}} w(e) \leq \sum_{e \in M^{\prime}}\left(\ell\left(e_{x}\right)+\ell\left(e_{y}\right)\right)\leq \sum_{v \in V} \ell(v) \] so $\sum_{v \in V} \ell(v)$ is an upper-bound on the cost of any perfect matching. Now let $M$ be a PM in $E_{\ell}$. Then $w(M)=\sum_{e \in M} w(e)=\sum_{v \in V} \ell(v)$ So $w\left(M^{\prime}\right) \leq w(M)$ and $M$ is optimal.

算法思路

This algorithm will be to Start with any feasible labeling $\ell$ and some matching $M$ in $E_{\ell}$ While $M$ is not perfect repeat the following:

Find an augmenting path for $M$ in $E_{\ell}$ this increases size of $M$
If no augmenting path exists, improve $\ell$ to $\ell^{\prime}$ such that $E_{\ell} \subset E_{\ell^{\prime}}$ Go to 1 Note that in each step of the loop we will either be increasing the size of $M$ or $E_{\ell}$ so this process must terminate.

Furthermore, when the process terminates, $M$ will be a perfect matching in $E_{\ell}$ for some feasible labeling $\ell$ So, by the Kuhn-Munkres theorem, $M$ will be a maxweight matching.

具体步骤

1.Finding an Initial Feasible Labelling--其中一边端点为0，另一边取节点连接边权重的最大值

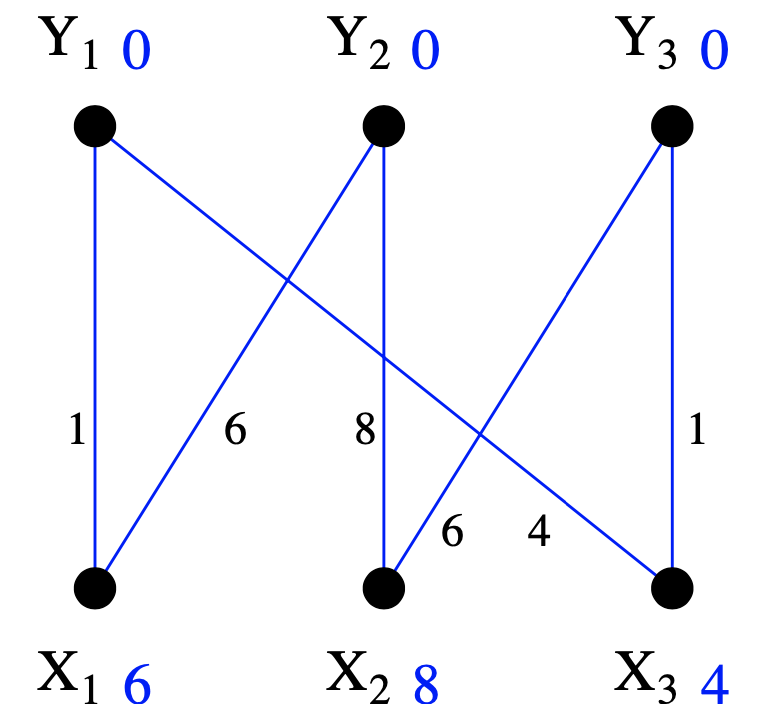
Finding an initial feasible labeling is simple. Just use:

\[ \forall y \in Y, \ell(y)=0, \quad \forall x \in X, \ell(x)=\max _{y \in Y}\{w(x, y)\} \]

With this labelling it is obvious that

\[ \forall x \in X, y \in Y, w(x) \leq \ell(x)+\ell(y) \]

2.Improving Labellings

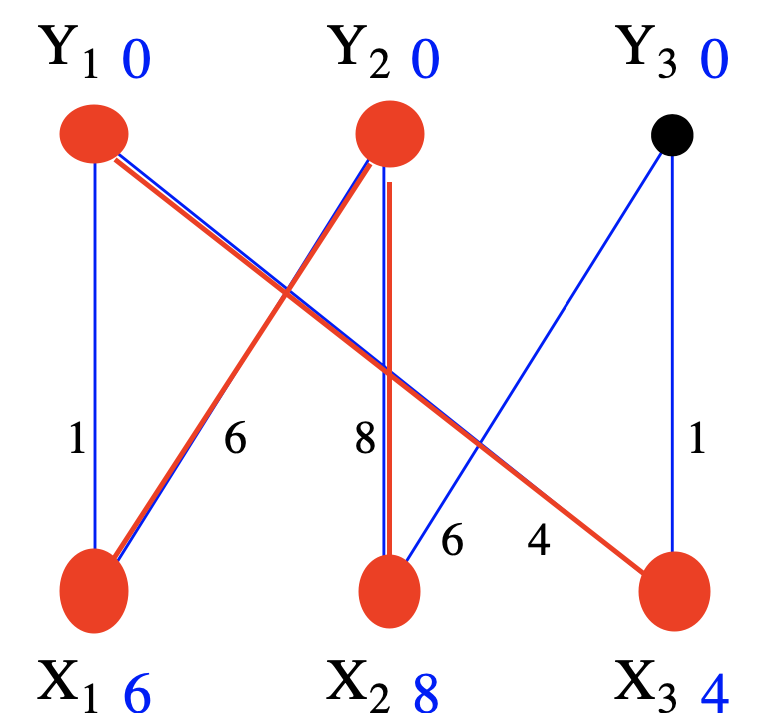
这是初始labeling产生的equality graph的$E_{\ell}$，节点和边用红色标注了出来. Note: 这个时候红色的图，只能找到最大匹配，形成不了完美匹配

扩展$E_{\ell} \subset E_{\ell^{\prime}}$ 的技巧

Let $\ell$ be a feasible labeling. Define neighbor of $u \in V$ and $\operatorname{set} S \subseteq V$ to be \[ N_{\ell}(u)=\left\{v:(u, v) \in E_{\ell},\right\}, \quad N_{\ell}(S)=\cup_{u \in S} N_{\ell}(u) \] Lemma: Let $S \subseteq X$ and $T=N_{\ell}(S) \neq Y.$ Set

Sen Yang Note: Bipartite graph：the neighbours of $x\in S$ are the $ yY$, so $T \subseteq Y$.

\[ \alpha_{\ell}=\min _{x \in S, y \notin T}\{\ell(x)+\ell(y)-w(x, y)\} \] and \[ \ell^{\prime}(v)=\left\{\begin{array}{ll} \ell(v)-\alpha_{\ell} & \text { if } v \in S \\ \ell(v)+\alpha_{\ell} & \text { if } v \in T \\ \ell(v) & \text { otherwise } \end{array}\right. \]

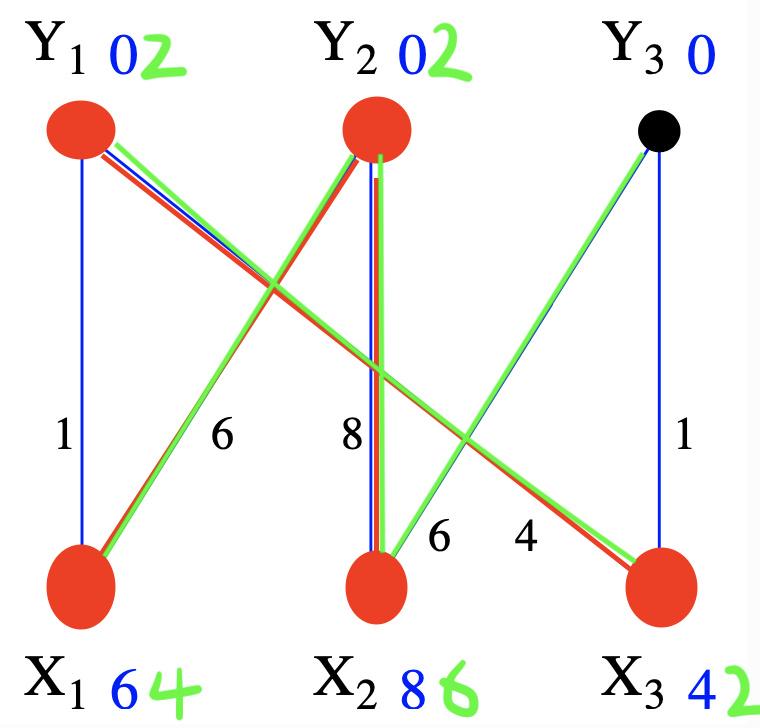
Sen Yang Note: 比如拿此时equality graph为例，$x \in S, y \notin T$的条件就是 $Y_3$和$X_2,X_3$,那么$\alpha_{\ell}=\min_{X_2,X_3,Y_3}\{8+0-6,4+0-1 \}=2$

然后上面构造$\ell^{\prime}(v)$的逻辑是，因为$S\cup T= E_{\ell}$，这样还能保证其中每个边对应labeling的和$\ell(v_S)-\alpha_{\ell}+\ell(v_T)+\alpha_{\ell}=\ell^{\prime}(v_S)+\ell^{\prime}(v_T)$依然是保持不变，那么原来属于,并且$Y$的label值增加，$X$的label值减少

Then $\ell^{\prime}$ is a feasible labeling and (i) If $(x, y) \in E_{\ell}$ for $x \in S, y \in T$ then $(x, y) \in E_{\ell^{\prime}}$ (ii) If $(x, y) \in E_{\ell}$ for $x \notin S, y \notin T$ then $(x, y) \in E_{\ell^{\prime}}$ (iii) There is some edge $(x, y) \in E_{\ell^{\prime}}$ for $x \in S, y \notin T$

Sen Yang Note:

(i)一定可以满足，（ii）不一定能找到这样的(x,y)比如当前的图中找不到一个$(x, y) \in E_{\ell}$ for $x \notin S, y \notin T$

（iii）多产生了一个新边 $(X_2, Y_3) \in E_{\ell^{\prime}}$，如下图。为什么会产生，这是因为我们$\alpha_{\ell}=\min_{X_2,X_3,Y_3}\{8+0-6,4+0-1 \}$

我们可以知道了这个

上面我们展示了扩展$E_{\ell} \subset E_{\ell^{\prime}}$ 的技巧，请注意，它并不是实际KM算法（Hungarian ）中的步骤，下面是真正的算法过程

KM算法：二分图加权最大匹配的匈牙利方法

整体思路

Generate initial labelling $\ell$ and matching $M$ in $E_{\ell}$
- If $M$ perfect, stop.
- Otherwise pick free vertex $u \in X$ $\operatorname{Set} S=\{u\}, T=\emptyset$
If $\left.N_{\ell}(S)=T, \text { update labels (forcing } N_{\ell}(S) \neq T\right)$ \[\begin{array}{l} \alpha_{\ell}=\min _{s \in S, y \notin T}\{\ell(x)+\ell(y)-w(x, y)\} \\ \ell^{\prime}(v)=\left\{\begin{array}{ll} \ell(v)-\alpha_{\ell} & \text { if } v \in S \\ \ell(v)+\alpha_{\ell} & \text { if } v \in T \\ \ell(v) & \text { otherwise } \end{array}\right. \end{array}\]
If $N_{\ell}(S) \neq T,$ pick $y \in N_{\ell}(S)-T$

If $ y$ free, $u-y$ is augmenting path. Augment $M$ and go to 2. Note that:增强路为什么会在这个时候产生？²
If $y$ matched, say to$z$, extend alternating tree: $S=S \cup\{z\}, T=T \cup\{y\} .$³ Go to 3

实战

迭代扩展匹配M至完美匹配

迭代等价图$E_l$

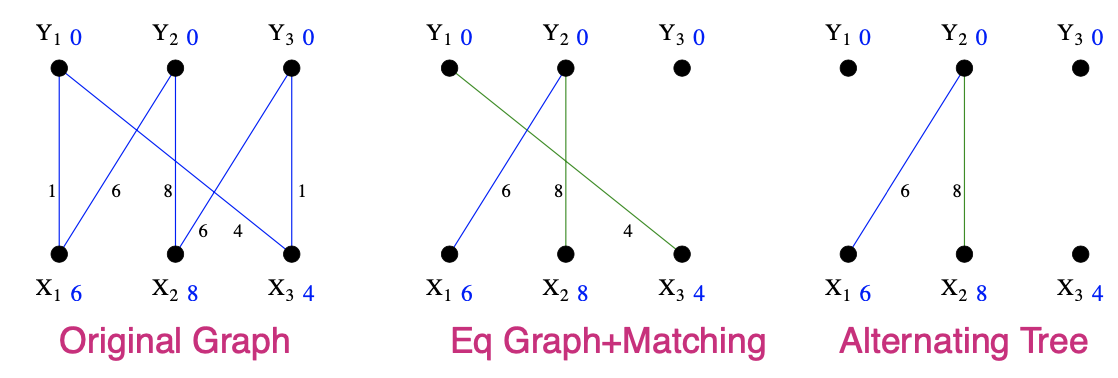
Initial Graph, trivial labelling and associated Equality Graph
Initial matching: $\left(x_{3}, y_{1}\right),\left(x_{2}, y_{2}\right)$ 初始的任意一种匹配M' $S=\left\{x_{1}\right\}, T=\emptyset$
since $N_{\ell}(S) \neq T,$ do step 4 Choose $y_{2} \in N_{\ell}(S)-T$
$y_{2}$ is matched so grow tree by adding $\left(y_{2}, x_{2}\right)$ ¡.e., $S=\left\{x_{1}, x_{2}\right\}, T=\left\{y_{2}\right\}$
At this point $N_{\ell}(S)=T,$ so goto 3

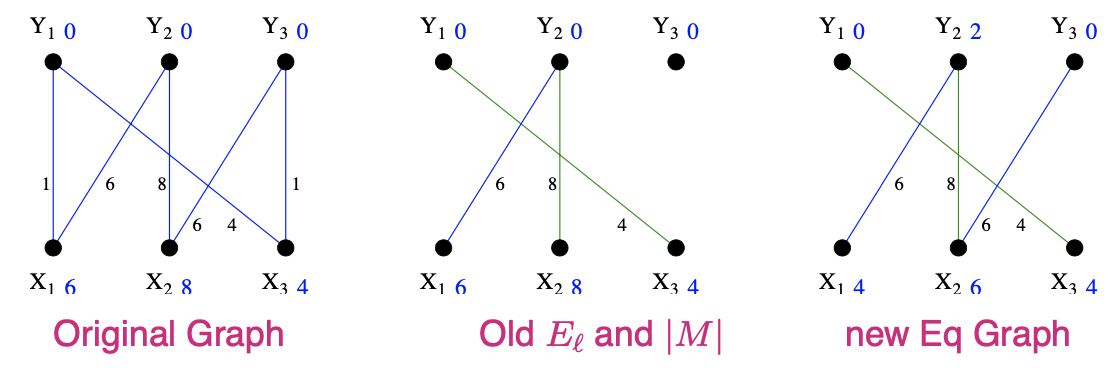
$S=\left\{x_{1}, x_{2}\right\}, T=\left\{y_{2}\right\}$ and $N_{\ell}(S)=T$
Calculate $\alpha_{\ell}$ \[ \begin{aligned} \alpha_{\ell} &=\min _{x \in S, y \notin T}\left\{\begin{array}{ll} 6+0-1, & \left(x_{1}, y_{1}\right) \\ 6+0-0, & \left(x_{1}, y_{3}\right) \\ 8+0-0, & \left(x_{2}, y_{1}\right) \\ 8+0-6, & \left(x_{2}, y_{3}\right) \end{array}\right.\\ &=2 \end{aligned} \]
Reduce labels of $S$ by 2

Increase labels of $T$ by 2
Now $N_{\ell}(S)=\left\{y_{2}, y_{3}\right\} \neq\left\{y_{2}\right\}=T$

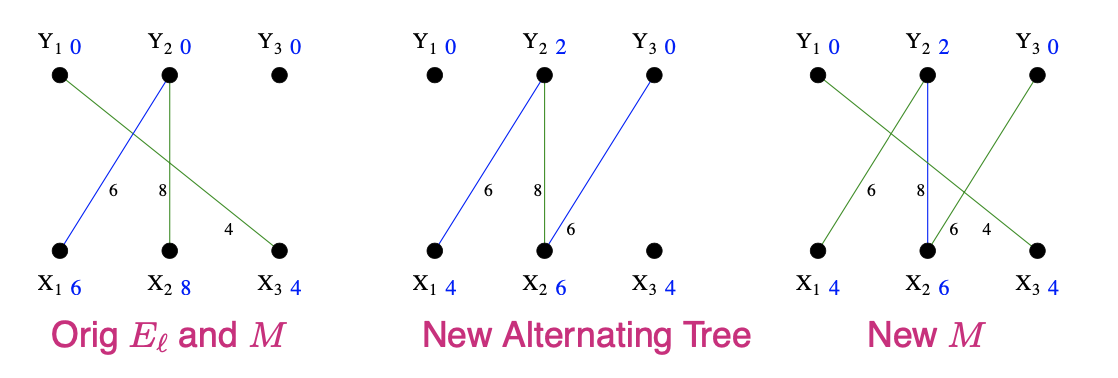
$\boldsymbol{S}=\left\{x_{1}, x_{2}\right\}, N_{\ell}(S)=\left\{y_{2}, y_{3}\right\}, T=\left\{y_{2}\right\}$
Choose $y_{3} \in N_{\ell}(S)-T$ and add it to $T$
$y_{3}$ is not matched in $M$ so we have just found an alternating path $x_{1}, y_{2}, x_{2}, y_{3}$ with two free endpoints. We can therefore augment $M$ to get a larger matching in the new equality graph. This matching is perfect, so it must be optimal.
Note that matching $\left(x_{1}, y_{2}\right),\left(x_{2}, y_{3}\right),\left(x_{3}, y_{1}\right)$ has cost $6+6+4=16$ which is exactly the sum of the labels in our final feasible labelling.

至此，我们从名词解释，到术语概念，到问题转换目标，到问题区分（二分图匹配和二分图加权最大匹配），到KM算法的原理与证明，再到算法步骤，最后举一个实际例分析，完整介绍了匈牙利算法。

后续，我们还会进一步研究匈牙利算法如何和一些CV任务进行结合。

实现-python

from munkres import Munkres

from scipy.optimize import linear_sum_assignment

参考文献

Munkres' Assignment Algorithm /Modified for Rectangular Matrices

Weighted Hungarian Algorithm

博主对KM的理解

建议阅读下面两个文档，从数学和算法的角度分析了加权二分图的最大权匹配问题

-数据结构与算法、组合优化的课程网站

Kuhn, H.W.: The hungarian method for the assignment problem (1955)↩
因为初始的$\operatorname{Set} S=\{u\}, T=\emptyset$ $u$是一个未匹配（free, 即不在$M$内）的一个顶点，而$y \in N_{\ell}(S)-T$表示此时M匹配（）的一个末端顶点又连接到的一个未匹配顶点，增广路形成了！增广路形成可以让我们的$M$匹配走向完美匹配！真的是太妙了！一定要注意到这一点。↩
扩展交替路的一种方法。添加的$S=S \cup\{z\}, T=T \cup\{y\},(z,y)$是一个匹配边↩

引言