My Findings - CoordConv坐标嵌入技术及其泛化性

posted on

Uber团队在2018NeurIPS上提出了CoordConv，它分析了卷积神经网络在进行坐标预测时存在的缺陷，并引入坐标嵌入方式来解决这个问题。但本人也注意到网上有人质疑这个方法，比如量子位小编报道了一个国外博主的质疑。本人看了他的质疑，他主要是在强调：

用完全数学的方式就可以构造出一个由one-hot heatmap映射到坐标的神经网络，并且根本不需要训练

实际上，他讲的这个和soft-argmax对heatmap求积分得到坐标的方法很像。首先，我想说，数学的归纳是一种非常高阶的手段和智能，很多问题本身就可以直接去用数学问题去解决，但是，这是直接注入了人类专家的知识，并不是神经网络本身从头学习到的（from scratch）。

CoordConv探讨的是，神经网络在拟合能力上以及泛化能力上存在的缺陷。CoorConv的亮点之一在于构造数据集划分的巧妙，一个是普通的train和test坐标数值分布一致的数据集，另外一个是test中的坐标取汁是train中完全没有的取值分布的数据集（正方形的1/4一角区域拿出来做测试），后者在考验模型在未见到的坐标分布上的泛化能力。

该论文的实验以及本人的实验验证发现，大多数普通的MLP或者Conv是很难调出一个好的泛化效果。而CoordConv神奇之处在于，它通过训练的方式来获取一种数学上的严格计算能力，结果确实做到了，因为train loss 和 test loss同时收敛到0，模型可以100%地精确预测坐标，这对于普通神经网络真的挺难的。

本文主要进行了如下的代码实验和分析：

  • 数据集：构造由坐标生成的one-hot heatmap与数值坐标之间的数据集：遵循An Intriguing Failing of Convolutional Neural Networks and the CoordConv Solution的quarter split方式。
  • 模型：利用神经网络加坐标嵌入（MLP+Coord and Conv+Coord）的方式进行拟合与泛化测试。
  • 效果分析与发现：用Pytorch复现验证了An Intriguing Failing of Convolutional Neural Networks and the CoordConv Solution中Superivised Coordinates Regression任务的CoordConv的泛化性能！
  • 可视化神经网络的某些层和输出，来发掘神经网络学习坐标信息的过程

数据集的构造

构造一个简单的数据集：由非归一化坐标构造表示位置的One-hot heatmap： \[ (x,y)\rightarrow H\in\mathbb{R}^{h\times w} \]

\[ H(j,i)=\left\{\begin{matrix} 1 & \text{if}\,\,i=x\wedge j=y\\ 0 & \text{if}\,\,i\neq x\vee j\neq y \end{matrix}\right. \]

其中，输入数据是\(H\),标签是\((x,y)\)

这个数据集还有一个特殊的部分就是train和test的划分。我们根据Coordconv论文，考虑了两种划分：

  • train set和test set采取uniform的位置数据采样
  • train set和test set采取quarter split的位置数据采样，即train set是在一个正方形内3/4区域内采样，test set在正方向剩下区域1/4采样

第二种数据集划分方式，更能考验模型的泛化性能，即在未见到的数据上的预测能力。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
import torch
import numpy as np
from skimage.filters import gaussian

h=64
w=64

def position(H, W, is_cuda=False):
    if is_cuda:
        loc_w = torch.linspace(-1.0, 1.0, W).cuda().unsqueeze(0).repeat(H, 1)
        loc_h = torch.linspace(-1.0, 1.0, H).cuda().unsqueeze(1).repeat(1, W)
    else:
        loc_w = torch.linspace(-1.0, 1.0, W).unsqueeze(0).repeat(H, 1)
        loc_h = torch.linspace(-1.0, 1.0, H).unsqueeze(1).repeat(1, W)
    loc = torch.cat([loc_w.unsqueeze(0), loc_h.unsqueeze(0)], 0)
    return loc


class heatmap_generator(torch.utils.data.Dataset):
    def __init__(self, size=(h, w), sigma=2, num=1000, is_train=True, uniform=False, seed=0, coordadd=False):
        super().__init__()
        self.dataset_size = num
        self.heatmap_size = size
        self.sigma = sigma
        self.is_train = is_train
        self.uniform = uniform
        self.coordadd = coordadd
        self.generator(seed, num)
        
    def generator(self,seed,num):
        torch.manual_seed(seed)
        np.random.seed(seed)
        
        self.db = []
        for i in range(num):
            heatmap = np.zeros(shape=self.heatmap_size, dtype=np.float32)
            if self.uniform:
                y = np.random.randint(self.heatmap_size[0])
                x = np.random.randint(self.heatmap_size[1])
            elif self.is_train:
                if np.random.rand() < 1/3:  # 1/3 probability: fall in this area
                    x = np.random.randint(0,  self.heatmap_size[1]/2)
                    y = np.random.randint(self.heatmap_size[0]/2, self.heatmap_size[0])
                else:
                    x = np.random.randint(self.heatmap_size[1])
                    y = np.random.randint(self.heatmap_size[0]/2)     
            else:
                y = np.random.randint(self.heatmap_size[0]/2, self.heatmap_size[0])
                x = np.random.randint(self.heatmap_size[1]/2, self.heatmap_size[1])
                
            heatmap[y,x] = 1
#             heatmap = gaussian(heatmap, sigma=self.sigma)
#             heatmap /= np.amax(heatmap)
            self.db.append(
                {
                    'heatmap':heatmap,
                    'pos': [x,y]  #[x/self.heatmap_size[1],y/self.heatmap_size[0]]
                })
  
    def __len__(self,):
        return self.dataset_size

    def __getitem__(self, idx):
        heatmap = self.db[idx]['heatmap']
        heatmap = torch.as_tensor(heatmap, dtype=torch.float32)
        pos = self.db[idx]['pos']
        pos = torch.as_tensor(pos, dtype=torch.float32)
        
        if self.coordadd:
            loc = position(heatmap.size(0), heatmap.size(1))
            heatmap = torch.cat([heatmap.unsqueeze(0), loc], dim=0) # [3,h,w]
        
        return heatmap, pos

import matplotlib.pyplot as plt

x=heatmap_generator(num=2, seed=0, is_train=True, coordadd=True)
d, _ = x[0]
d = d.numpy()
print(d.shape)
figs, axs = plt.subplots(1,3)
axs.flat[0].imshow(d[0], cmap='jet')
axs.flat[1].imshow(d[1], cmap='jet')
axs.flat[2].imshow(d[2], cmap='jet')
plt.show()
(3, 64, 64)
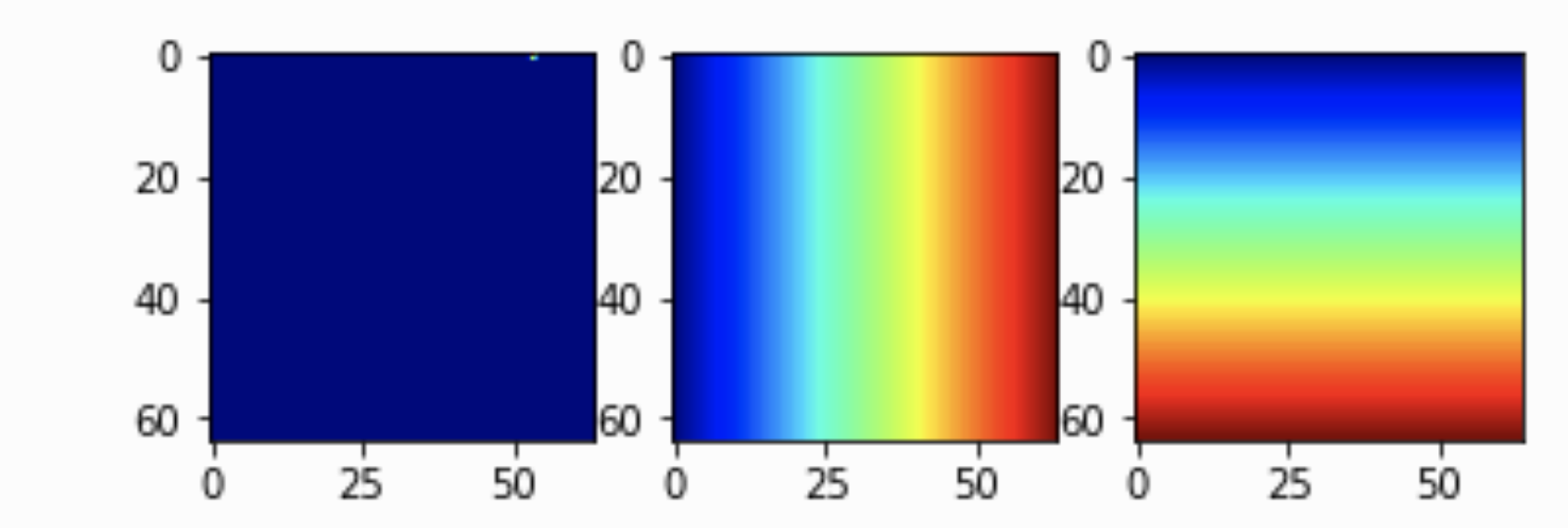
image-20200922211840620
image-20200922211840620

上面三幅图从左至右分别是：

  • 构造的表示坐标位置的One-hot heatmap编码；
  • 在x方向上的坐标信息嵌入，取值在[-1,1]
  • 在y方向上的坐标信息嵌入，取值在[-1,1]

MLP预测坐标的能力怎么样

一开始，我们最直接的想法就是，构造一个简单的多层感知机MLP做直接的映射:从one-hot heatmap 到 \((x,y)\)。

代码很简单：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class net(nn.Module):
    def __init__(self, input_dim, h, output_dim):
        super().__init__()
        self.l = nn.Sequential(
            nn.Linear(input_dim, h),
            nn.LayerNorm(h),
            nn.ReLU(),
            nn.Linear(h, h),
            nn.LayerNorm(h),
            nn.ReLU(),
            nn.Linear(h, output_dim),
            
        )
       
    def forward(self, x):
        x = x.flatten(1)
        return self.l(x).sigmoid()

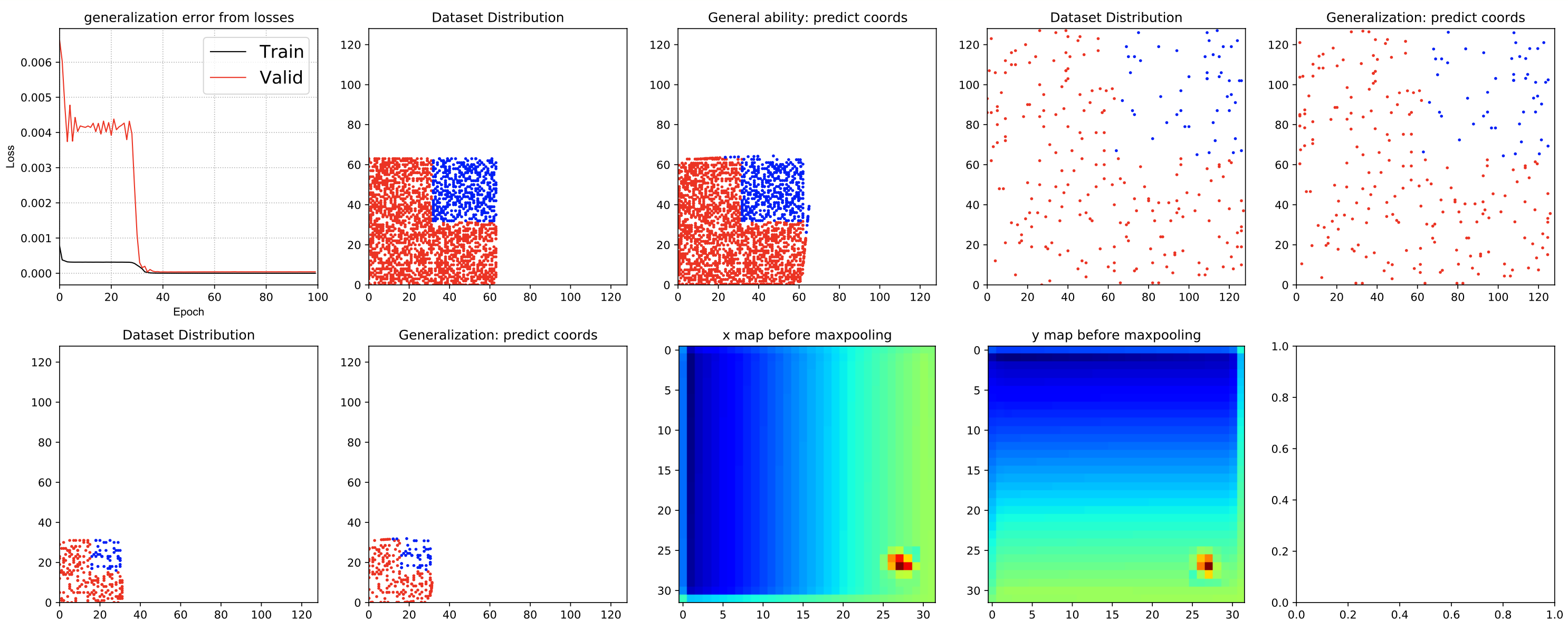
然后我们用Uniform的数据集划分进行训练测试。结果如下：

image-20201205141125263image-20201205141136074

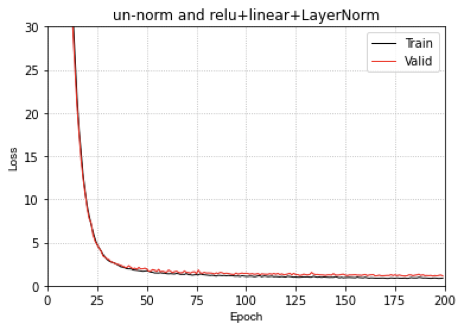
image-20201205141202969image-20201205141153742

我们看一下MLP在Uniform数据集划分上的预测结果

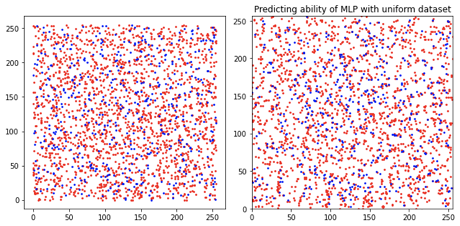
image-20201205142413078
image-20201205142413078

左图是数据集的位置的真实分布（红色是Train set，蓝色是test set），右图是MLP的预测结果。

从上面的结果上来看，对于一致分布的数据集，整体上，MLP的表现似乎还可以，

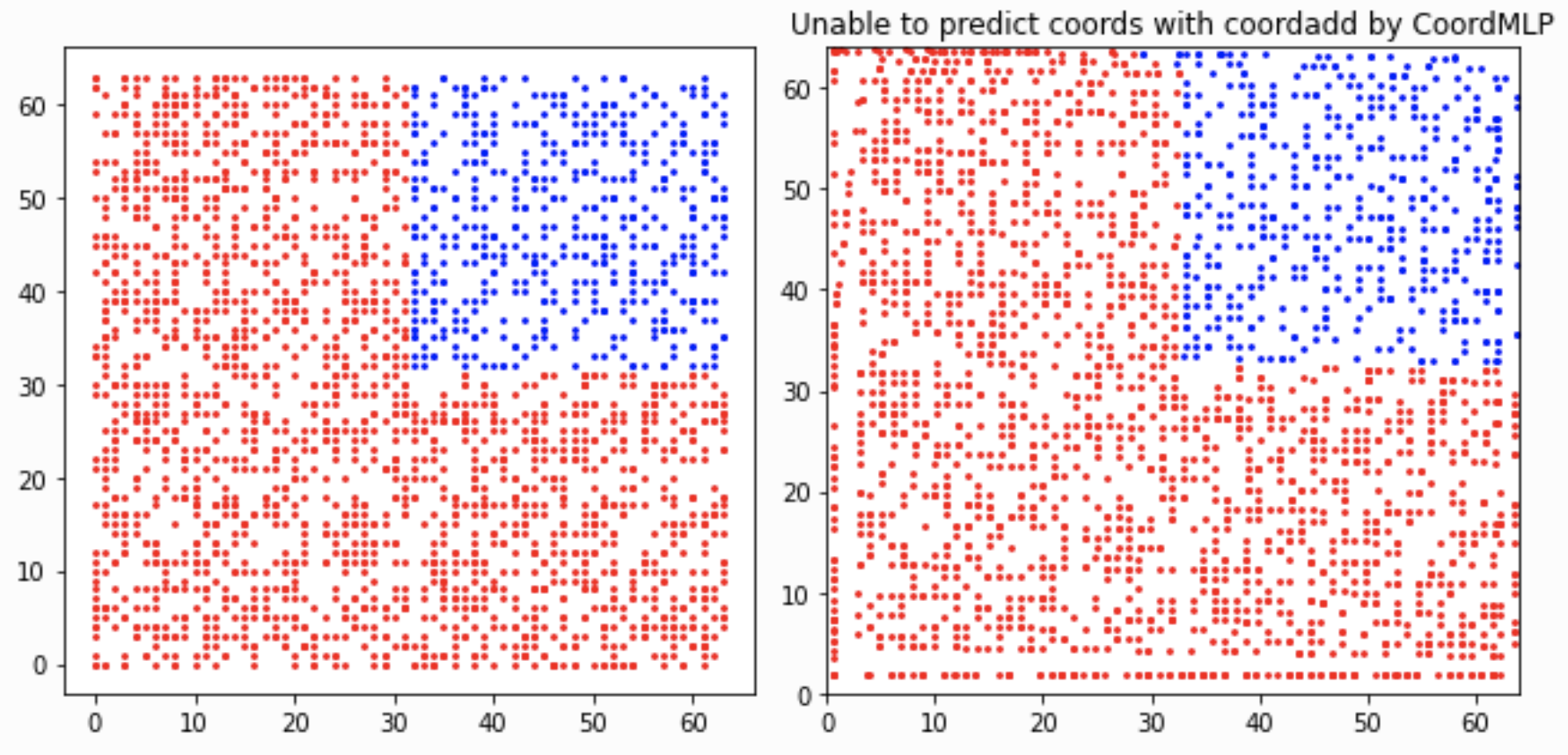
那如果换成Quarter Split划分的数据集会怎么样呢？

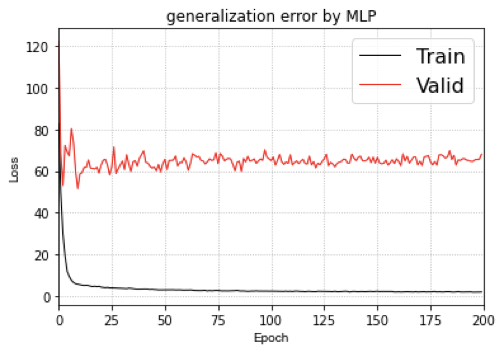
image-20201205141335408

好像MLP就无法具备泛化特性了矣？

Traing loss和Valid loss（就是test集合）的差距（泛化误差）很大，

我们再看看预测的结果。

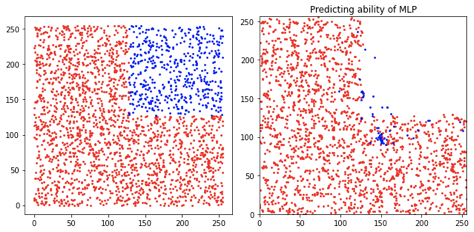
image-20201205142120386
image-20201205142120386

左图是数据集的位置的真实分布（红色是Train set，蓝色是test set），右图是MLP的预测结果。

这一结果更加印证了，MLP完全只是过拟合了Train set，而不真正具备了位置预测的能力。

而对于Uniform的数据集的样本分布，Test和Train的分布几乎一致，MLP所谓的预测坐标，只是因为它“见过”类似的样本，“学习了”它该输出什么才能“满足loss小的需求”！

那我们是不是可以给MLP加入坐标嵌入技术来改进提升其泛化能力？

CoordMLP 怎么样？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
import torch.nn as nn
import os
class net(nn.Module):
    def __init__(self, input_dim, h, output_dim):
        super().__init__()
        self.l = nn.Sequential(
            nn.Linear(input_dim, h),
            nn.LayerNorm(h),
            nn.ReLU(),
            nn.Linear(h, h),
            nn.LayerNorm(h),
            nn.ReLU(),
            nn.Linear(h, output_dim),
            
        )
       
    def forward(self, x):
        x = x.flatten(1)
        return self.l(x).sigmoid()
    
class convnet(nn.Module):
    def __init__(self, img_size, h, output_dim):
        super().__init__()
        self.conv = nn.Conv2d(3,h,kernel_size=3,padding=1)
        dim = img_size[0]*img_size[1]*h
        self.l = nn.Sequential(
            nn.Linear(dim, h),
            nn.LayerNorm(h),
            nn.ReLU(),
            nn.Linear(h, h),
            nn.LayerNorm(h),
            nn.ReLU(),
            nn.Linear(h, output_dim),
            
        )
       
    def forward(self, x):
        
        return self.l(x).sigmoid()

os.environ['CUDA_VISIBLE_DEVICES'] = "0,1"
    
train_set = heatmap_generator(num=2000, seed=0, is_train=True, coordadd=True)
valid_set = heatmap_generator(num=500, seed=1, is_train=False, coordadd=True)
test_set = heatmap_generator(num=1000, seed=2, is_train=False, coordadd=True)

train_loader = torch.utils.data.DataLoader(train_set, batch_size=64, drop_last=False, shuffle=True)
valid_loader = torch.utils.data.DataLoader(valid_set, batch_size=64, drop_last=False)
test_loader = torch.utils.data.DataLoader(test_set, batch_size=64, drop_last=False)


length = 3*h*w
model = net(length, 256, 2).cuda()
epochs = 200
criterion = nn.L1Loss(reduction='mean').cuda()

optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

train_losses = []
valid_losses = []
for e in range(epochs):
    model.train()
    t = 0
    n1 = 0
    for id, (heatmaps, coords) in enumerate(train_loader):
        heatmaps, coords = heatmaps.cuda(), coords.cuda()
        optimizer.zero_grad()
        
        out = model(heatmaps)
        wh = torch.tensor([w,h]).unsqueeze(0).to(out.device) 
        out = out*wh
        coords[:,0]  = coords[:,0] * w
        coords[:,1]  = coords[:,1] * h
        
        loss = criterion(out, coords)
        loss.backward()
        optimizer.step()
        t +=loss.item()
        n1 +=1
        if id%5 ==0:
            print("[{}/{}]:train loss:{:.3f}".format(e,id,loss.item()))
            
    train_losses.append(t/n1)
    v = 0
    n2 = 0
    model.eval()
    for id, (heatmaps, coords) in enumerate(valid_loader):
        heatmaps, coords = heatmaps.cuda(), coords.cuda()
        out = model(heatmaps)
        
        wh = torch.tensor([w,h]).unsqueeze(0).to(out.device)      
        out = out*wh     
        coords[:,0]  = coords[:,0] * w
        coords[:,1]  = coords[:,1] * h
        
        loss = criterion(out, coords)
        v +=loss.item()
        n2 +=1
        if id%5 ==0:
            print("[{}/{}]:valid loss:{:.3f}".format(e,id,loss.item()))
    
    valid_losses.append(v/n2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
[0/0]:train loss:66.604
[0/5]:train loss:56.174
[0/10]:train loss:62.741
[0/15]:train loss:61.951
[0/20]:train loss:54.515
[0/25]:train loss:56.364
[0/30]:train loss:56.916
[0/0]:valid loss:85.686
[0/5]:valid loss:86.086
[1/0]:train loss:55.726
[1/5]:train loss:62.358
[1/10]:train loss:65.846
[1/15]:train loss:59.389
[1/20]:train loss:62.986
[1/25]:train loss:63.098
[1/30]:train loss:58.376
[1/0]:valid loss:93.375
[1/5]:valid loss:93.775
[2/0]:train loss:61.380
[2/5]:train loss:61.412
[2/10]:train loss:58.127
[2/15]:train loss:60.215
[2/20]:train loss:59.366
[2/25]:train loss:58.879
[2/30]:train loss:60.355
[2/0]:valid loss:91.508
[2/5]:valid loss:91.908
[3/0]:train loss:60.517
[3/5]:train loss:55.383
[3/10]:train loss:63.124
[3/15]:train loss:56.669
[3/20]:train loss:62.911
[3/25]:train loss:62.907
[3/30]:train loss:51.110
[3/0]:valid loss:87.514
[3/5]:valid loss:87.915
[4/0]:train loss:54.624
[4/5]:train loss:59.512

.....

.....

.....
[194/20]:train loss:13.425
[194/25]:train loss:8.053
[194/30]:train loss:19.025
[194/0]:valid loss:77.454
[194/5]:valid loss:76.766
[195/0]:train loss:28.187
[195/5]:train loss:19.203
[195/10]:train loss:9.961
[195/15]:train loss:8.364
[195/20]:train loss:17.076
[195/25]:train loss:20.528
[195/30]:train loss:8.590
[195/0]:valid loss:80.181
[195/5]:valid loss:80.544
[196/0]:train loss:10.859
[196/5]:train loss:9.294
[196/10]:train loss:19.587
[196/15]:train loss:23.072
[196/20]:train loss:9.886
[196/25]:train loss:20.046
[196/30]:train loss:17.368
[196/0]:valid loss:98.249
[196/5]:valid loss:98.891
[197/0]:train loss:17.661
[197/5]:train loss:16.903
[197/10]:train loss:16.224
[197/15]:train loss:14.529
[197/20]:train loss:12.648
[197/25]:train loss:16.197
[197/30]:train loss:20.337
[197/0]:valid loss:89.428
[197/5]:valid loss:90.051
[198/0]:train loss:8.844
[198/5]:train loss:8.096
[198/10]:train loss:5.853
[198/15]:train loss:12.344
[198/20]:train loss:7.346
[198/25]:train loss:14.299
[198/30]:train loss:20.001
[198/0]:valid loss:65.037
[198/5]:valid loss:64.701
[199/0]:train loss:13.411
[199/5]:train loss:14.213
[199/10]:train loss:10.256
[199/15]:train loss:17.550
[199/20]:train loss:19.302
[199/25]:train loss:14.925
[199/30]:train loss:14.372
[199/0]:valid loss:74.663
[199/5]:valid loss:75.049
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import matplotlib as mpl
mpl.style.use('seaborn-bright')
fig = plt.figure()

epochnum = list(range(0,len(train_losses)))

plt.plot(epochnum, train_losses, color='black', linewidth=1)
plt.plot(epochnum, valid_losses, color='red',linewidth=1)
plt.xlabel('Epoch', fontdict={'family':'Arial'})
plt.ylabel('Loss',fontdict={'family':'Arial'})
plt.xlim(0, len(train_losses))
plt.ylim(0,100)
#plt.xticks(epochnum,100*list(epochnum) )
plt.legend(('Train',
            'Valid'), loc='best',fontsize=16)
plt.title("generalization error with coordadd by CoordMLP")

plt.grid(linestyle=':')

plt.show()

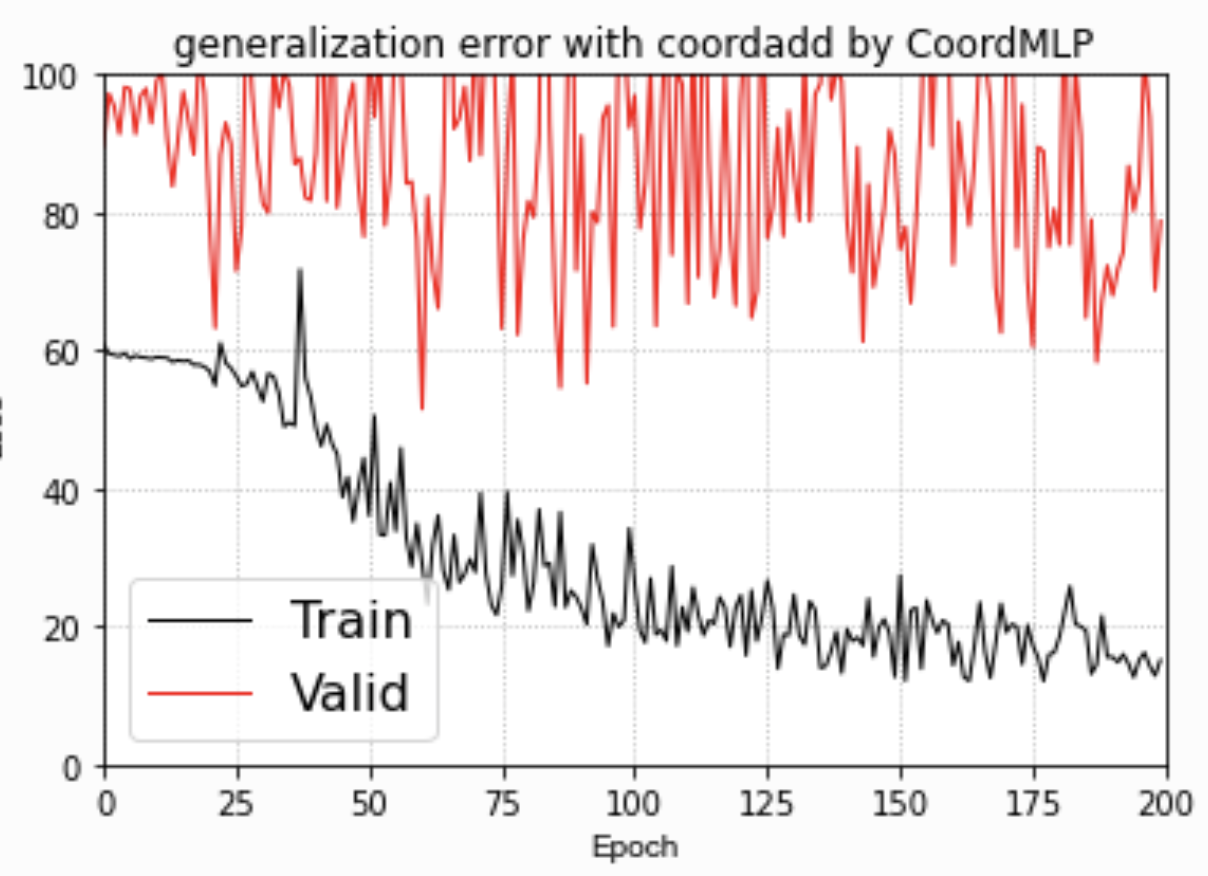
image-20200922211620495

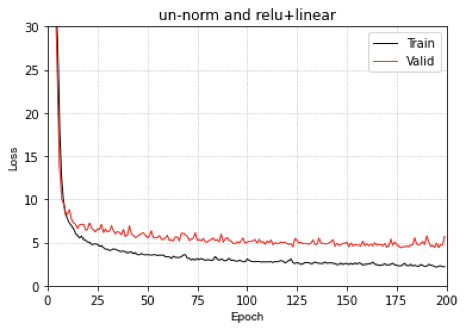
根据Loss看来，CoordMLP 嵌入坐标信息的MLP还是不具备好的泛化能力！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
fig, ax1 = plt.subplots()
fig2, ax2 = plt.subplots()
print(model)

for k, p in model.state_dict().items():
    print(k)
    #print(p)
    if 'weight' in k:
        layer = k.split('.')[1]
        for i in p:
            #
            if i.dim() > 0 :
                for z in range(10):
                    ax1.scatter(layer, i[z].item(), s=1.5)
            else:
                ax1.scatter(layer, i.item(), s=1.5)
                
    if 'bias' in k:
        layer = k.split('.')[1]
        for i in p:
            #
            if i.dim() > 0 :
                for z in range(10):
                    ax2.scatter(layer, i[z].item(), s=1.5)
            else:
                ax2.scatter(layer, i.item(), s=1.5)
    
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
net(
  (l): Sequential(
    (0): Linear(in_features=196608, out_features=256, bias=True)
    (1): LayerNorm((256,), eps=1e-05, elementwise_affine=True)
    (2): ReLU()
    (3): Linear(in_features=256, out_features=256, bias=True)
    (4): LayerNorm((256,), eps=1e-05, elementwise_affine=True)
    (5): ReLU()
    (6): Linear(in_features=256, out_features=2, bias=True)
  )
)
l.0.weight
l.0.bias
l.1.weight
l.1.bias
l.3.weight
l.3.bias
l.4.weight
l.4.bias
l.6.weight
l.6.bias

image-20200922211705256

可视化MLP的权重参数

通过可视化MLP权重参数的取值，我们发现了不同层的取值范围的分布是不同的

但是并没有获得什么有意义的信息和解释

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
train_set = heatmap_generator(num=2000, seed=0, uniform=True)
valid_set = heatmap_generator(num=500, seed=1, uniform=True)

fig, ax = plt.subplots(1, 2)

for heatmap, pos in train_set:
    x = pos[0]*w
    y = pos[1]*h
    ax[0].scatter(x, y, c='red', s=3)

for heatmap, pos in valid_set:
    x = pos[0]*w
    y = pos[1]*h
    ax[0].scatter(x, y, c='blue', s=3)



plt.xlim(0, w)
plt.ylim(0, h)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
train_set = heatmap_generator(num=2000, seed=0, is_train=True, coordadd=True)
valid_set = heatmap_generator(num=500, seed=1, is_train=False, coordadd=True)

fig, ax = plt.subplots(1, 2, figsize=(9, 4.5), tight_layout=True)

model.cuda()

for heatmap, pos in train_set:
    x = pos[0]
    y = pos[1]
    ax[0].scatter(x, y, c='red', s=3)
    out = model(heatmap.flatten(0).unsqueeze(0).cuda()).squeeze().detach().cpu().numpy()
    x = out[0]
    y = out[1]
    ax[1].scatter(x, y, c='red', s=3)

for heatmap, pos in valid_set:
    x = pos[0]
    y = pos[1]
    ax[0].scatter(x, y, c='blue', s=3)
    out = model(heatmap.flatten(0).unsqueeze(0).cuda()).squeeze().detach().cpu().numpy()
    x = out[0]
    y = out[1]
    ax[1].scatter(x, y, c='blue', s=3)


plt.xlim(0, w)
plt.ylim(0, h)
plt.title("Unable to predict coords with coordadd by CoordMLP")
plt.show()
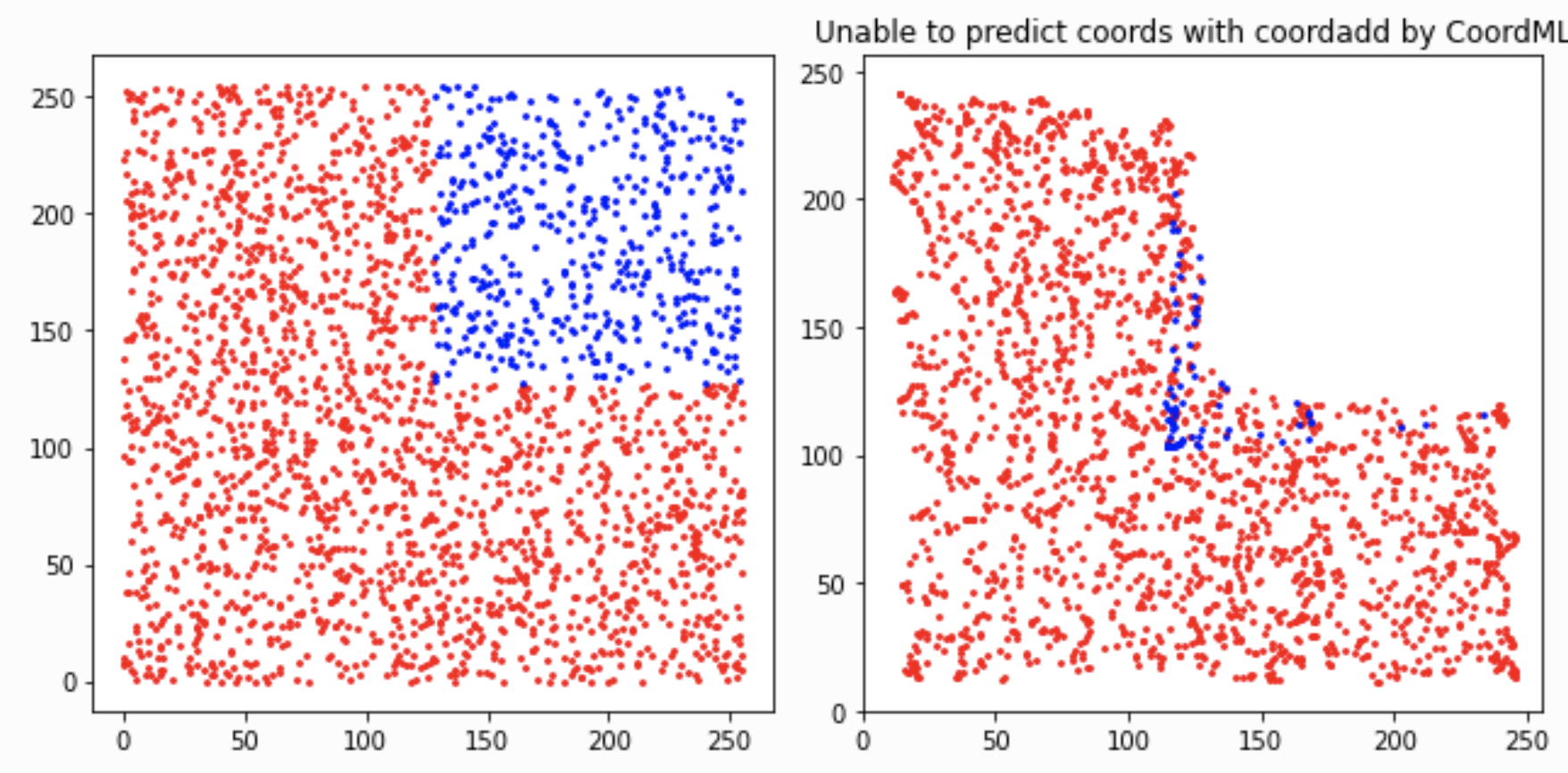
image-20200922211731117
image-20200922211731117

嵌入坐标信息的CoordMLP 像单纯的MLP一样，好像也不具备预测坐标的泛化性能

把heatmap嵌入Coordinate Maps，然后Flatten，然后送进MLP中，模型可以在训练集上预测得很好，但是却不具备泛化能力。可以看到，这种训练和验证集的Quart split划分方式还是非常有趣，并且是有难度的。

CoordConv 怎么样呢？

接下来我用PyTorch复现下面这个论文的部分内容。

An Intriguing Failing of Convolutional Neural Networks and the CoordConv Solution论文提出了一种坐标嵌入的方法

我们根据论文官方放出的Tensorflow代码，用PyTorch严格按照其网络结构重写。训练的优化器、学习率及其weight decay也尽可能和它保持一致。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
import torch
import torch.nn as nn
import torch.nn.functional as F
import os
from coordconv import CoordConv1d, CoordConv2d, CoordConv3d

class convnet1(nn.Module):
    def __init__(self):
        super(convnet1, self).__init__()
        self.coordconv = CoordConv2d(1, 8, 1, with_r=True)
        self.conv1 = nn.Conv2d(8, 8, 1)
        self.conv2 = nn.Conv2d(8, 8, 1)
        self.conv3 = nn.Conv2d(8, 8, 1)
        self.conv4 = nn.Conv2d(8, 8, 3, padding=1)
        self.conv5 = nn.Conv2d(8, 2, 3, padding=1)
        self.pool = nn.MaxPool2d(kernel_size=64, stride=64)

    def forward(self, x):
        x = x.unsqueeze(1)
        x = self.coordconv(x)
        x = self.conv1(x)
        x = self.conv2(x)
        x = self.conv3(x)
        x = self.conv4(x)
        x = self.conv5(x)
        x = self.pool(x)  # [bs, 2, 1, 1]
        x = x.squeeze()
        return x

os.environ['CUDA_VISIBLE_DEVICES'] = "0"

train_set = heatmap_generator(num=2000, seed=0, is_train=True,) # coordadd=True)
valid_set = heatmap_generator(num=500, seed=1, is_train=False,) # coordadd=True)
test_set = heatmap_generator(num=1000, seed=2, is_train=False,) # coordadd=True)

train_loader = torch.utils.data.DataLoader(train_set, batch_size=256, drop_last=False, shuffle=True)
valid_loader = torch.utils.data.DataLoader(valid_set, batch_size=32, drop_last=False)
test_loader = torch.utils.data.DataLoader(test_set, batch_size=32, drop_last=False)

model = convnet1().cuda()
epochs = 1000
criterion = nn.MSELoss(reduction='mean').cuda()

optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=0.00001)

train_losses = []
valid_losses = []
for e in range(epochs):
    model.train()
    t = 0
    n1 = 0
    for id, (heatmaps, coords) in enumerate(train_loader):
        heatmaps, coords = heatmaps.cuda(), coords.cuda()
        optimizer.zero_grad()
        
        out = model(heatmaps)
        
        loss = criterion(out, coords)
        loss.backward()
        optimizer.step()
        
        t +=loss.item()
        n1 +=1
        if id%100 ==0:
            print("[{}/{}]:train loss:{:.3f}".format(e,id,loss.item()))
            
    train_losses.append(t/n1)
    v = 0
    n2 = 0
    model.eval()
    for id, (heatmaps, coords) in enumerate(valid_loader):
        heatmaps, coords = heatmaps.cuda(), coords.cuda()
        out = model(heatmaps)
        
        loss = criterion(out, coords)
        v +=loss.item()
        n2 +=1
        if id%100 ==0:
            print("[{}/{}]:valid loss:{:.3f}".format(e,id,loss.item()))
    
    valid_losses.append(v/n2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
[0/0]:train loss:1027.723
[0/0]:valid loss:658.191
[1/0]:train loss:340.205
[1/0]:valid loss:882.184
[2/0]:train loss:382.191
[2/0]:valid loss:364.457
[3/0]:train loss:344.636
[3/0]:valid loss:629.423
[4/0]:train loss:343.474
[4/0]:valid loss:511.996
[5/0]:train loss:310.839
[5/0]:valid loss:521.019
[6/0]:train loss:330.839
[6/0]:valid loss:530.305
[7/0]:train loss:310.050
[7/0]:valid loss:500.017
[8/0]:train loss:313.915
[8/0]:valid loss:526.495
[9/0]:train loss:335.083
[9/0]:valid loss:578.623
[10/0]:train loss:321.808
[10/0]:valid loss:590.830
[11/0]:train loss:332.714
[11/0]:valid loss:520.583
[12/0]:train loss:315.320
[12/0]:valid loss:506.796
[13/0]:train loss:329.973
[13/0]:valid loss:516.331
[14/0]:train loss:296.927
[14/0]:valid loss:440.843
[15/0]:train loss:319.363
[15/0]:valid loss:565.522
[16/0]:train loss:339.193
[16/0]:valid loss:630.012
[17/0]:train loss:319.562
[17/0]:valid loss:588.987
[18/0]:train loss:325.077
[18/0]:valid loss:555.196
[19/0]:train loss:324.888
[19/0]:valid loss:504.099
[20/0]:train loss:328.839
[20/0]:valid loss:501.208
[21/0]:train loss:322.016

​
​ ......

​
​ ......

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
[489/0]:train loss:313.746
[489/0]:valid loss:498.646
[490/0]:train loss:331.695
[490/0]:valid loss:570.283
[491/0]:train loss:308.808
[491/0]:valid loss:543.668
[492/0]:train loss:331.526
[492/0]:valid loss:609.543
[493/0]:train loss:314.055
[493/0]:valid loss:530.251
[494/0]:train loss:303.886
[494/0]:valid loss:557.143
[495/0]:train loss:321.458
[495/0]:valid loss:543.295
[496/0]:train loss:311.247
[496/0]:valid loss:497.568
[497/0]:train loss:326.582
[497/0]:valid loss:515.231
[498/0]:train loss:333.465
[498/0]:valid loss:553.942
[499/0]:train loss:308.450
[499/0]:valid loss:573.775
[500/0]:train loss:304.610
[500/0]:valid loss:585.026
[501/0]:train loss:325.851
[501/0]:valid loss:577.704
[502/0]:train loss:313.319
[502/0]:valid loss:510.165
[503/0]:train loss:301.331
[503/0]:valid loss:563.254
[504/0]:train loss:294.513
[504/0]:valid loss:550.867
[505/0]:train loss:337.322
[505/0]:valid loss:405.499
[506/0]:train loss:210.640
[506/0]:valid loss:440.354
[507/0]:train loss:177.821
[507/0]:valid loss:372.500
[508/0]:train loss:152.111
[508/0]:valid loss:314.090
[509/0]:train loss:150.206
[509/0]:valid loss:531.095
[510/0]:train loss:131.546
[510/0]:valid loss:320.094
[511/0]:train loss:124.478
[511/0]:valid loss:348.056
[512/0]:train loss:82.704
[512/0]:valid loss:138.187
[513/0]:train loss:93.763
[513/0]:valid loss:59.943
[514/0]:train loss:28.917
[514/0]:valid loss:83.261
[515/0]:train loss:26.591
[515/0]:valid loss:103.014
[516/0]:train loss:20.655
[516/0]:valid loss:90.283
[517/0]:train loss:14.670
[517/0]:valid loss:86.509
[518/0]:train loss:7.979
[518/0]:valid loss:81.485
[519/0]:train loss:5.293
[519/0]:valid loss:82.389
[520/0]:train loss:6.404
[520/0]:valid loss:79.925
[521/0]:train loss:4.992
[521/0]:valid loss:73.615
[522/0]:train loss:2.514
[522/0]:valid loss:68.852
[523/0]:train loss:3.168
[523/0]:valid loss:61.463
[524/0]:train loss:2.194
[524/0]:valid loss:58.418
[525/0]:train loss:3.485
[525/0]:valid loss:55.320
[526/0]:train loss:2.697
[526/0]:valid loss:46.612
[527/0]:train loss:4.031
[527/0]:valid loss:42.675
[528/0]:train loss:3.537
[528/0]:valid loss:35.026
[529/0]:train loss:2.433
[529/0]:valid loss:21.490
[530/0]:train loss:1.950
[530/0]:valid loss:6.599
[531/0]:train loss:1.498
[531/0]:valid loss:0.874
[532/0]:train loss:0.641
[532/0]:valid loss:0.786
[533/0]:train loss:1.632
[533/0]:valid loss:0.256
[534/0]:train loss:0.318
[534/0]:valid loss:1.699
[535/0]:train loss:3.042
[535/0]:valid loss:1.706
[536/0]:train loss:1.189
[536/0]:valid loss:1.651
[537/0]:train loss:4.311
[537/0]:valid loss:1.211
[538/0]:train loss:2.011
[538/0]:valid loss:4.156
[539/0]:train loss:2.527
[539/0]:valid loss:1.380
[540/0]:train loss:1.754
[540/0]:valid loss:7.980
[541/0]:train loss:4.717
[541/0]:valid loss:7.452
[542/0]:train loss:2.004
[542/0]:valid loss:0.953
[543/0]:train loss:1.676
[543/0]:valid loss:0.460
[544/0]:train loss:1.610
[544/0]:valid loss:0.386
[545/0]:train loss:0.336
[545/0]:valid loss:0.584

​
​ ...... ​
​ ......

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
[992/0]:train loss:0.056
[992/0]:valid loss:0.034
[993/0]:train loss:0.034
[993/0]:valid loss:0.043
[994/0]:train loss:0.051
[994/0]:valid loss:0.050
[995/0]:train loss:0.041
[995/0]:valid loss:0.061
[996/0]:train loss:0.108
[996/0]:valid loss:0.389
[997/0]:train loss:0.539
[997/0]:valid loss:0.133
[998/0]:train loss:0.250
[998/0]:valid loss:0.107
[999/0]:train loss:0.247
[999/0]:valid loss:1.734

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import matplotlib as mpl
mpl.style.use('seaborn-bright')
fig = plt.figure()

epochnum = list(range(0,len(train_losses)))

plt.plot(epochnum, train_losses, color='black', linewidth=1)
plt.plot(epochnum, valid_losses, color='red',linewidth=1)
plt.xlabel('Epoch', fontdict={'family':'Arial'})
plt.ylabel('Loss',fontdict={'family':'Arial'})
plt.xlim(0, len(train_losses))

plt.legend(('Train',
            'Valid'), loc='best',fontsize=16)
plt.title("generalization error with coordadd by CoordConv")

plt.grid(linestyle=':')

plt.show()
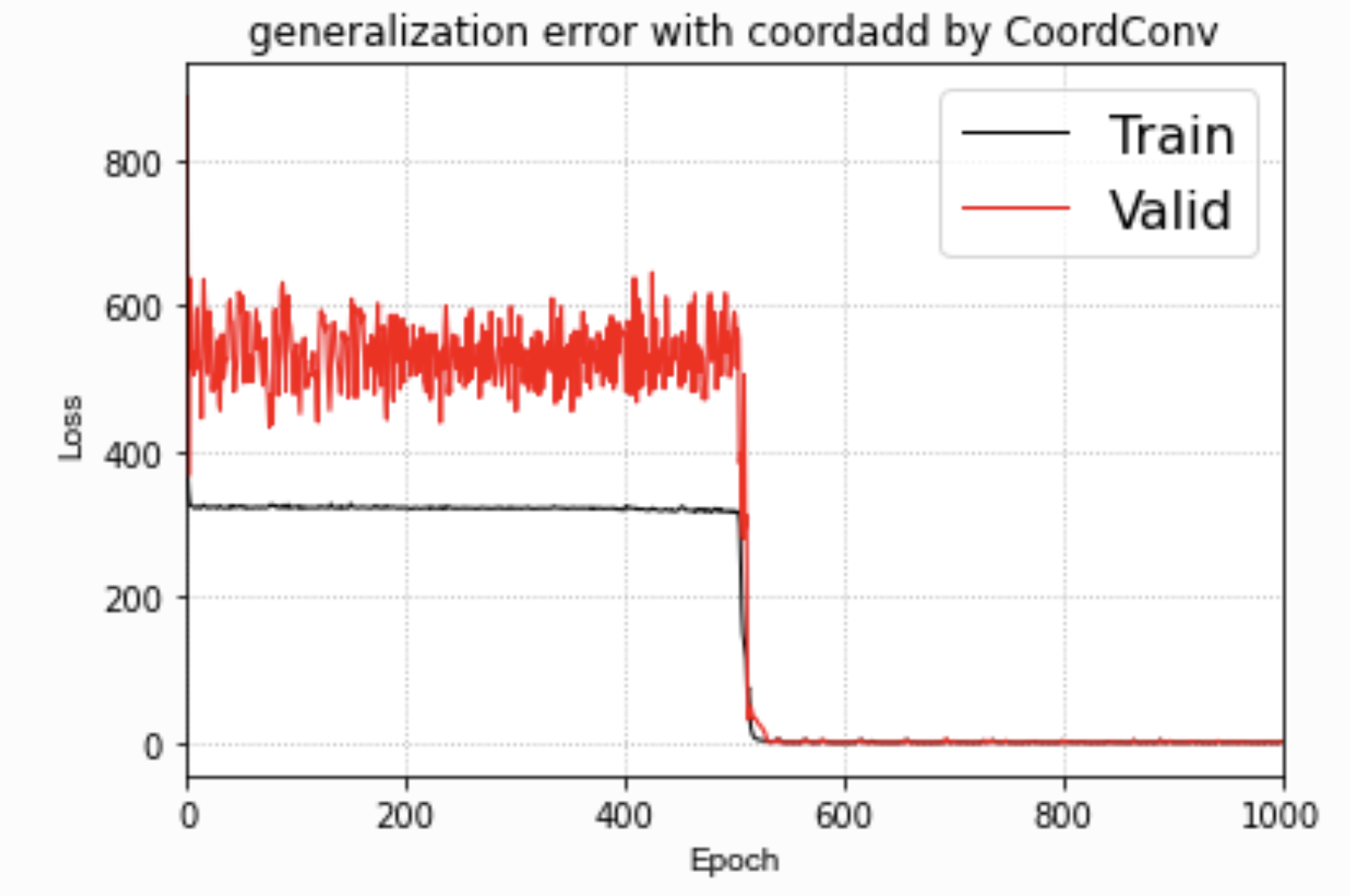
image-20200922211755053
image-20200922211755053

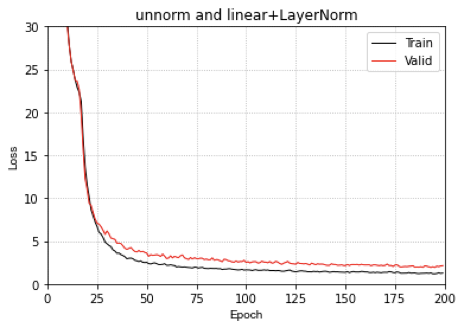
我有了一个神奇的发现，在500个周期后，train和test loss开始急速收敛！？

500个周期时，训练loss和验证的loss，开始极速下降！

我怀疑这个代价函数的优化曲面有一个非常难以跳出的局部最优解，因为我的训练集和验证集的数据分布之间有一个非常明显的GAP！

如果能有人看到这个, 对这个问题有自己的见解，欢迎和我探讨！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
fig, ax = plt.subplots(1, 2, figsize=(9, 4.5), tight_layout=True)

model.cuda()

for heatmap, pos in train_set:
    x = pos[0]
    y = pos[1]
    ax[0].scatter(x, y, c='red', s=3)
    out = model(heatmap.unsqueeze(0).cuda()).squeeze().detach().cpu().numpy()
    x = out[0]
    y = out[1]
    ax[1].scatter(x, y, c='red', s=3)

for heatmap, pos in valid_set:
    x = pos[0]
    y = pos[1]
    ax[0].scatter(x, y, c='blue', s=3)
    out = model(heatmap.unsqueeze(0).cuda()).squeeze().detach().cpu().numpy()
    x = out[0]
    y = out[1]
    ax[1].scatter(x, y, c='blue', s=3)


plt.xlim(0, w)
plt.ylim(0, h)
plt.title("Unable to predict coords with coordadd by CoordMLP")
plt.show()
image-20200922211812693
image-20200922211812693

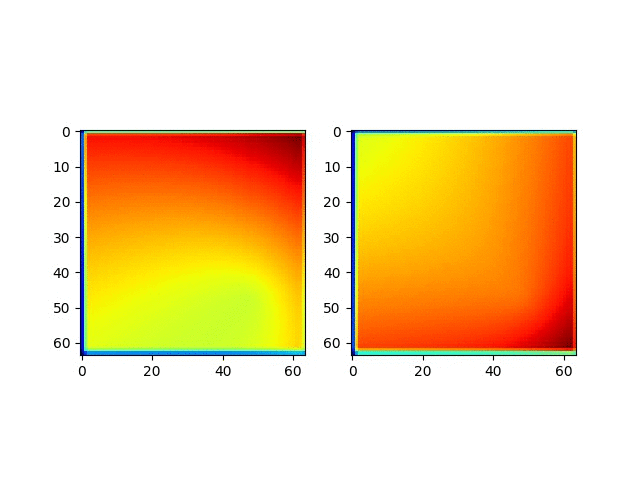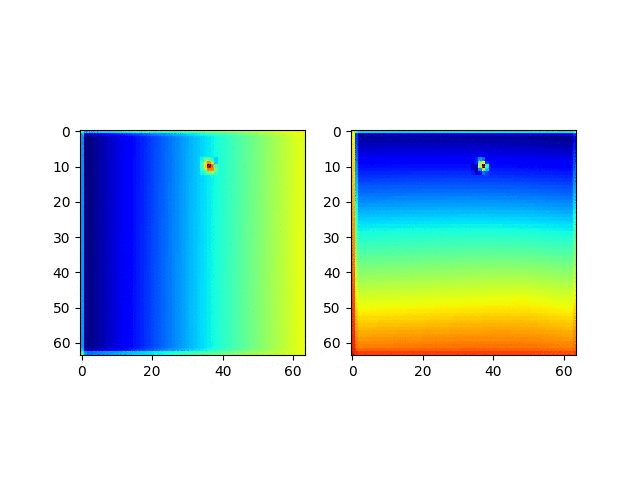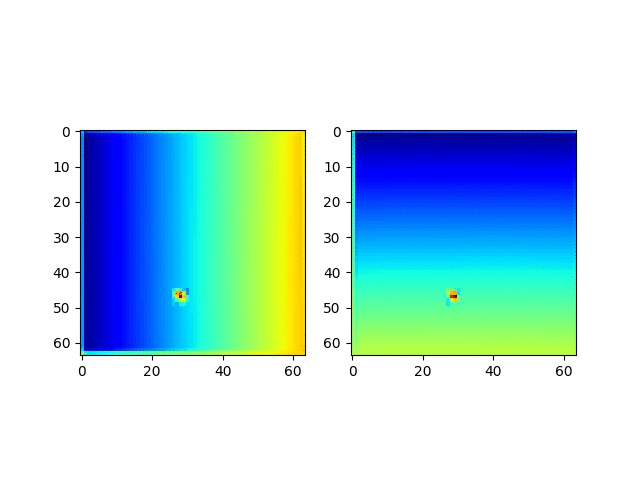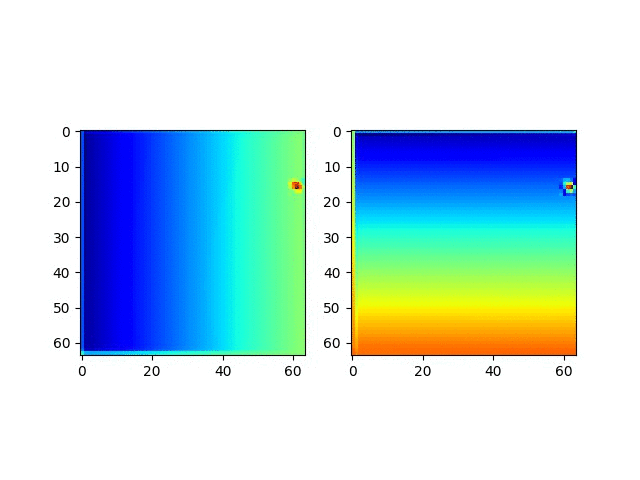
我们继续看一看CoordConv预测的坐标实际是什么样的。

很明显，这个CoordConv的网络具备了非常神奇的预测位置的能力。

并且获取这个坐标回归能力是突然在某个周期获得的！！！

我个人猜测，这个代价函数的优化曲面有一个很深的局部最小值点。Adam不断积累的梯度跳出了它。PS：这个问题在我用了更小的权重衰减之后，就解决了，CoordConv很快收敛。

论文回顾

In this work, we expose and analyze a generic inability of CNNs to transform spatial representations between two different types: from a dense Cartesian representation to a sparse, pixel-based represen- tation or in the opposite direction. Though such transformations would seem simple for networks to learn, it turns out to be more difficult than expected, at least when models are comprised of the commonly used stacks of convolutional layers. While straightforward stacks of convolutional layers excel at tasks like image classification, they are not quite the right model for coordinate transform.

Throughout the rest of the paper, we examine the coordinate transform problem starting with the simplest scenario and ending with the most complex. Although results on toy problems should generally be taken with a degree of skepticism, starting small allows us to pinpoint the issue, exploring and understanding it in detail. Later sections then show that the phenomenon observed in the toy domain indeed appears in more real-world settings.

We begin by showing that coordinate transforms are surprisingly difficult even when the problem is small and supervised. In the Supervised Coordinate Classification task, given a pixel’s (x, y) coordinates as input, we train a CNN to highlight it as output. The Supervised Coordinate Regression task entails the inverse: given an input image containing a single white pixel, output its coordinates. We show that both problems are harder than expected using convolutional layers but become trivial by using a CoordConv layer (Section 4).

Some Tricks and Visualizations：

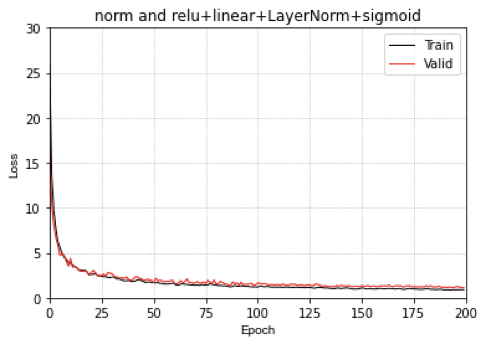
我改进CoordConv时用到了以下的一些Tricks：

  • 在靠近网络输出层之前，增加CoordConv层能够显著提升收敛速度
  • 坐标归一化
  • 数值尺度控制（可以获得更强的泛化特性，即对于未见到不同大小的Heatmap具备泛化特性！）

CoordConv在相同优化条件下，只用了100个周期内就很快收敛，并且获得了很强的泛化能力。

还进行了

  • pooling前 map的可视化
  • CoordConv在不同大小的one-hot heatmap的数据集的泛化能力测试

100个周期

image-20200924145925184
image-20200924145925184

本文正文到此结束，后面还会继续研究，欢迎讨论，可联系我的邮箱yangsenius@seu.edu.cn

【本人原创，转发请注明来源】

「Sen Yang. The findings on CoordConv technique. https://senyang-ml.github.io/2020/09/22/coordconv/, 2020」