G-RMI-> PersonLab -> PifPaf Composite Fields for Human Pose Estimation - CVPR 2019 论文解读
博客地址：https://yangsenius.github.io/blog/2-pifpaf/
arxiv地址: https://arxiv.org/abs/1903.06593 github地址: https://github.com/vita-epfl/openpifpaf
今年的CVPR19的论文最近已经在CVF Openaccess 网站上放出来了。
还记得去年18CVPR论文出来的时候，我把所有有关的人体姿态估计的论文的题目和概要大致都看了，得出的一个浅显的结论就是：3D姿态估计、密集姿态估计要流行起来了。这是因为在去年CVPR18的论文中，出现了大量的3D有关的论文而少有2D姿态估计研究（比如在MPII, COCO keypoint数据集上的方法挺少，可能2d姿态的都去发了ECCV18）。
而今年19CVPR的姿态估计好像又呈现出一次小爆发
COCO数据集上的性能又来到了一次新高：似乎74mAP已经被突破了（HRNet, 0.770 mAP, ECSI, 0.746 mAP）。。。
各位研究者们，是不是感觉到了精度上、性能上的压力。。。深度调参还是方法革新，这是个问题.
众多论文中，我先阅读了这篇，OpenPIFPAF。 因为它奇怪的名字好像是茫茫论文海中出现的那个与众不同的一篇，吸引我去一探Ta的全貌与究竟
读完后，我觉得OpenPifpaf继承了几篇姿态估计论文的工作：
- openpose
- G-RMI
- PersonLAB (应该说大部分核心的想法来自于PersonLab)
并致力于解决几个棘手的问题： - Bottom-up的多人姿态解析问题 - 自动驾驶中，图像中小尺寸人体的问题
其实很有必要介绍一下先前的工作
G-RMI
G-RMI 是google的一篇自上而下处理姿态估计问题的开篇
通过Faster-RCNN检测得到包含单个人体的bounding box，然后再进行单人姿态估计
本论文在预测\(K\)个表示置信度的heatmaps之外，又引入了offset fields的方法，用\(2\times K\)个heatmaps表示，即每个heatmap的位置上预测一个\(F_k(x_{i})=l_k-x_{i}\)的位移偏量，用\(l_k\)来表示真实位置，其中\(x_i,k \in \mathbb{Z}_+^2\) \(i,k\)表示位置索引和关键点类型。
\[ h_{k}\left(x_{i}\right)=1 \text { if }\left\|x_{i}-l_{k}\right\| \leq R \]
\[ F_k(x_{i})=l_k-x_{i} \] After generating the heatmaps and offsets, we aggregate them to produce highly localized activation maps \(f_{k}\left(x_{i}\right)\) as follows: \[ f_{k}\left(x_{i}\right)=\sum_{j} \frac{1}{\pi R^{2}} G\left(x_{j}+F_{k}\left(x_{j}\right)-x_{i}\right) h_{k}\left(x_{j}\right) \]
其中第三个公式中的\(G(\cdot)\)论文中说它是双线性插值核，并用霍夫投票的形式。在今年19CVPR的openpifpaf论文，又再次利用这个公式，不过用一个高斯核来代替了\(G(\cdot)\)函数，我从中推断出这是起到了平滑取值的作用，就像我们在构造产生grountruth heatmaps那样的做法。下面的\(\pi R^{2}\)是一个归一化，和高斯核那样类似。
注：这个\(G(\cdot)\)函数其实是很多人理解这篇论文的绊脚石。实际上,这就是对上采样后的heatmaps再次进行一次平滑.
A different approach addressing this issue would be to predict activation maps,as in [27], which allow for multiple predictions of the same keypoint. However, the size of the activation maps, and thus the localization precision, is limited by the size of the net’s output feature maps, which is a fraction of the input imagesize, due to the use of max-pooling with decimation.In order to address the above limitations, we adopt acombined classification and regression approach. For each spatial position, we first classify whether it is in the vicin-ity of each of the K keypoints or not (which we call a “heatmap”), then predict a 2-D local offset vector to get amore precise estimate of the corresponding keypoint loca-tion. Note that this approach is inspired by work on object detection, where a similar setup is used to predict bounding boxes, e.g. [14, 37]. Figure 2 illustrates these three output channels per keypoint.
训练loss是：
\[ L(\theta)=\lambda_{h} L_{h}(\theta)+\lambda_{o} L_{o}(\theta) \]
\(\lambda_{h}=4\) and \(\lambda_{o}=1\) is a scalar factor to balance.
We use a single ResNet model with two convolutional output heads. The output of the firshead passes through a sigmoid function to yield the heatmap probabilities \(h_{k}\left(x_{i}\right)\) for each position \(x_{i}\) and each keypoint \(k\) . The training target \(\overline{h}_{k}\left(x_{i}\right)\) is a map of zeros and ones, with \(\overline{h}_{k}\left(x_{i}\right)=1\) if \(\left\|x_{i}-l_{k}\right\| \leq R\) and 0 otherwise. The corresponding loss function \(L_{h}(\theta)\) is the sum of logistic losses for each position and keypoint separately.
\[ L_{o}(\theta)=\sum_{k=1 : K} \sum_{i :\left\|l_{k}-x_{i}\right\| \leq R} H\left(\left\|F_{k}\left(x_{i}\right)-\left(l_{k}-x_{i}\right)\right\|\right) \]
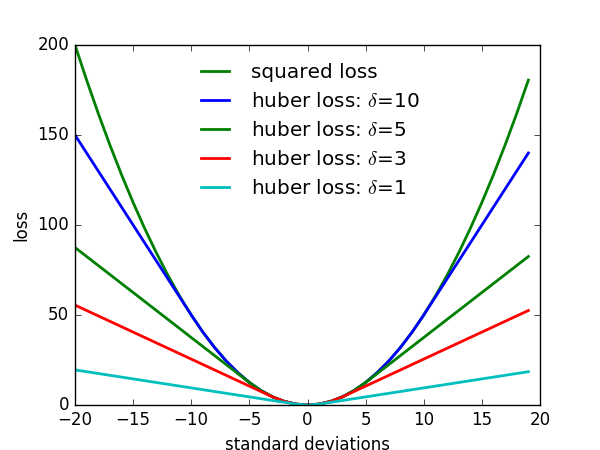
where \(H(u)\) is the Huber robust loss, \(l_{k}\) is the position of the \(k\) -th keypoint, and we only compute the loss for positions \(x_{i}\) within a disk of radius \(R\) from each keypoint.
Huber robust loss的函数图像为：
G-RMI的开创行思路:keypoints location disk mask logistic classication and short-range offset解决了下采样导致对量化误差问题!!
作者构造出0,1取值构成的kepoints location masks heatmaps和某关键点对应对heatmap的每个grid位置相对于其真实位置的偏移的分类加回归预测方法!!
这一点PersonLab和PifPaf都沿袭了这一思路
而PersonLab在此基础上,为了解决多人关联肢体的算法设计问题,又继续引入了mid-range pairwise offset来针对instance association这一问题, 可以说将将G-RMI的方法拓展到多人问题上.
PersonLab
PersonLab在构造监督标签和网络预测表示上面下了不少功夫。 公式总览：
\(\textbf{K heatmaps: } \qquad\qquad\qquad\qquad\qquad p_{k}(x)=1 \text { if } x \in \mathcal{D}_{R}\left(y_{j, k}\right), \mathcal{D}_{R}(y)=\{x :\|x -y\| \leq R\}\)
\(\textbf{K short-range 2-D offset fields: } \qquad S_{k}(x)=y_{j, k}-x\)
\(\textbf{K Hough score maps: }\qquad \qquad \qquad h_{k}(x)=\frac{1}{\pi R^{2}} \sum_{i=1 : N} p_{k}\left(x_{i}\right) B\left(x_{i}+S_{k}\left(x_{i}\right)-x\right)\)
\(\textbf{2(K-1) mid-range 2-D offset fields: }\quad M_{k, l}(x)=\left(y_{j, l}-x\right)\left[x \in \mathcal{D}_{R}\left(y_{j, k}\right)\right], \text{from k-th to l-th}\)
\(\textbf{K long-range 2-D offset fields: }\qquad \qquad L_{k}(x)=y_{j, k}-x\)
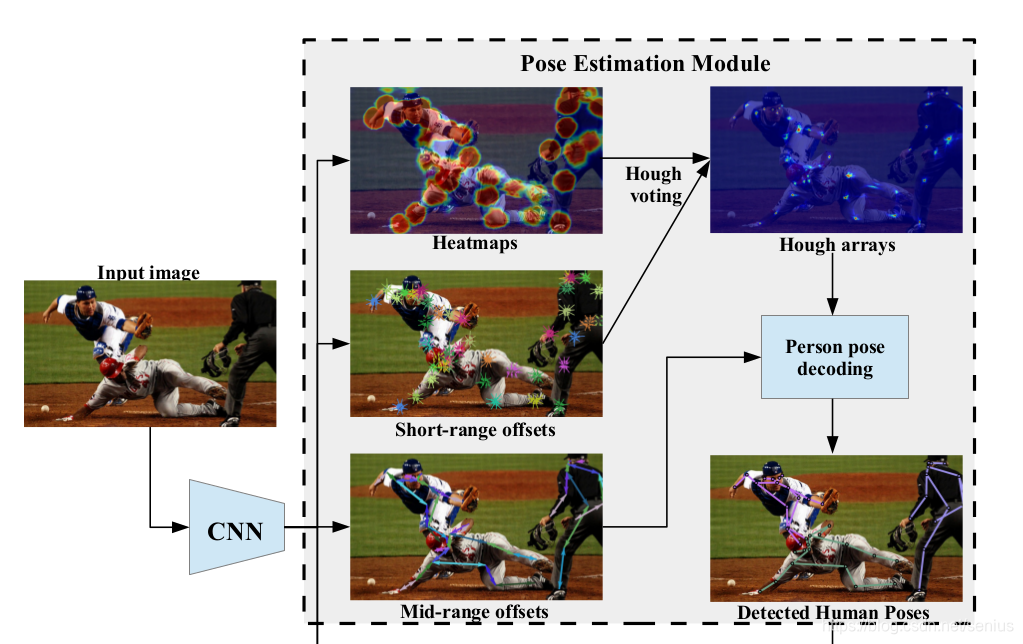在Personlab中,\(h_k(x)\),即hough投票后对高精度score maps并不提供实例相关的信息, 而需要一种机制来group together the keypoints belonging to each individual instance. 因此, 作者继续构造了mid-range pairwise offeset 负责connect the dots.
mid-range pairwise offeset 也是 2D的offset fields: \(M_{k, l}(x)\) > We compute 2\((K-1)\) such offset fields, one for each directededge connecting pairs \((k, l)\) of keypoints which are adjacent to each other in a tree-structured kinematic graph of the person, see Figs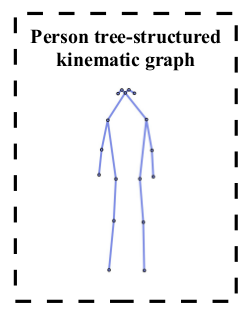 
这里的2\((K-1)=2\times16\) 个向量场指的是 上图16种肢体连接的正反2种方向:\((k,l)和(l,k)\)的偏移向量场 \(M_{k, l}(x)=\left(y_{j, l}-x\right)\left[x \in \mathcal{D}_{R}\left(y_{j, k}\right)\right]\) , 这个向量场还是在disk对半径范围内的.
Recurrent offset refinement： 作者在预测一些大尺寸人体时,有时候mid-range pairwise offsets很长,精度可能不准,所以用了Recurrent offset refinement:
\[ M_{k, l}(x) \leftarrow x^{\prime}+S_{l}\left(x^{\prime}\right), \text { where } x^{\prime}=M_{k, l}(x), \] 来进一步提高精度,迭代2次上述对公式. 其中,\(S_{l}\left(x^{\prime}\right)\)是short-range offset.
Fast greedy decoding
有了所有人体的关键点的预测位置和每个关键点的mid-range pairwise offset, 接下来要做的就是 进行将属于同一个人体的关键点组合成一个实例的机制。
PersonLab 构造出一个优先级的队列，根据Hough score maps \(h_{k}(x)\)上的局部最大值的位置（这里强调局部最大值，是因为可能会有false positive 的位置）以及其score高于一定的阈值的（实验取0.01） 来按得分大小顺序放入队列，这些放入队列中的关键点应该被称为了seed点（pifpaf实际上没有解释清楚这个seed点），从最高响应值的seed点位置开始，以此不断找到其在tree-structure上的连接关键点。
在这个算法迭代的每一步中，如果发现当前的seed关键点落入了已经关联到先前某个人体\(j^{\prime},\)的某个\(k\)类型对seed关键点的 \(\mathcal{D}_{r}\left(y_{j^{\prime}, k}\right)\) 半径内，那么就意味着，这个半径区域内有可能有两个同样类型的关键点，那么我们就可以开辟一个新的人体实例\(j\),作为另外一个人体的\(k\)类型关键点作为seed. 其中,通过seed点计算与其adjacent的关键点的公式是:\(y_{j, l}=y_{j, k}+M_{k, l}\left(y_{j, k}\right)\).
这种机制对于所有关键点的是公平的,即 根据高得分的关键点位置作为起始seed,(我想起了Associative Embedding 对待起始点是从头部开始), 然而实际中容易检测的点往往是起始位置点, 这种方法能够一定程度处理遮挡问题.
the position \(x_{i}\) of the current candidate detection seed of type \(k\) is within a disk \(\mathcal{D}_{r}\left(y_{j^{\prime}, k}\right)\) of the corresponding keypoint of previously detected person instances \(j^{\prime},\) then we reject it;
Personlab的decoding 大致代码如下: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135 config.EDGES = [
(0, 14),
(0, 13),
(0, 4),
(0, 1),
(14, 16),
(13, 15),
(4, 10),
(1, 7),
(10, 11),
(7, 8),
(11, 12),
(8, 9),
(4, 5),
(1, 2),
(5, 6),
(2, 3)
]
def group_skeletons(keypoints, mid_offsets):
# keypoints 是hough score maps 所有局部最大值位置产生对所有候选关键点
# keypoints 数组每个元素为{'xy':[x,y],'id':k,'conf':score}
keypoints.sort(key=(lambda kp: kp['conf']), reverse=True)
# 按照从大到小排序
skeletons = []
# skeletons 表示多个人体骨架,每个元素是单人的骨架坐标集合
# config.EDGES 表示16个单向的骨架连接边,dir_edges 构造出双向的连接边
dir_edges = config.EDGES + [edge[::-1] for edge in config.EDGES]
# 为每个关键点生成跟它相连的关键点的集合,比如 左肘部有[左肩膀,左手腕]
skeleton_graph = {i:[] for i in range(config.NUM_KP)}
for i in range(config.NUM_KP):
for j in range(config.NUM_KP):
if (i,j) in config.EDGES or (j,i) in config.EDGES:
skeleton_graph[i].append(j)
skeleton_graph[j].append(i)
# 优先级队列
while len(keypoints) > 0:
# pop出最大置信度的候选关键点
kp = keypoints.pop(0)
# 判断该类型(根据id)关键点有没有落入了之前的某个骨架的同类关键点上
# 计算距离是否在r=10(论文里面提到)内
if any([np.linalg.norm(kp['xy']-s[kp['id'], :2]) <= 10 for s in skeletons]):
# 如果是,则抑制该关键点(非极大值抑制)
# 如果否，则认为该类型关键点属于另外一个人体，那么就开辟新的实例
continue
# 构造新的骨架
this_skel = np.zeros((config.NUM_KP, 3))
# 将该类型关键点的坐标和置信度赋值给该骨架
this_skel[kp['id'], :2] = kp['xy']
this_skel[kp['id'], 2] = kp['conf']
# 此处 引入该函数
###########################
def iterative_bfs(graph, start, path=[]):
'''iterative breadth first search from start'''
# 此处的graph是所有的每个关键点与它相连的关键点的构成的多叉树结构
# start 表示关键点的类型
# 构造队列
q=[(None,start)]
visited = []
while q:
# 拿出第一个元素v (关键点l（子点）,关键点k（父点）) 初始 关键点l=None
v=q.pop(0)
# 如果其对应的关键点k之前没访问过
if not v[1] in visited:
# 记录访问
visited.append(v[1])
# 记录路径
path=path+[v]
# 将在图结构graph中,找到关键点k直接相连的所有子关键点k_1,k_2,...
# 放到队列中[(关键点l_1关键点k_1),(关键点l_2,关键点k_2),...]
q=q+[(v[1], w) for w in graph[v[1]]]
# 然后子点变成父点，下一次迭代生出更多的子点
# 循环,这样的话,不论初始点是什么,我们都可以找到一个包含完整人体树结构tree-structure的路径,
# 包含所有 [(None,关键点k),(关键点k,关键点k_1),(关键点1_x,关键点k_2),...,(关键点16_x,关键点16)] 一共会有17个path, 然而就会多余出1个连接,就是初始连接.
return path
#假如是Lwrist 为起始点的话: path=[('Lwrist', 'Lelbow'), ('Lelbow', 'Lshoulder'), ('Lshoulder', 'nose'), ('Lshoulder', 'Lhip'), ('nose', 'Rshoulder'), ('nose', 'Reye'), ('nose', 'Leye'), ('Lhip', 'Lknee'), ('Rshoulder', 'Relbow'), ('Rshoulder', 'Rhip'), ('Reye', 'Rear'), ('Leye', 'Lear'), ('Lknee', 'Lankle'), ('Relbow', 'Rwrist'), ('Rhip', 'Rknee'), ('Rknee', 'Rankle')]
###########################
# 此处对skeleton_graph是每个关键点与它相连的关键点的图结构
path = iterative_bfs(skeleton_graph, kp['id'])[1:] # 此处1:开始,即去掉多余的连接
for edge in path:
# 判断第一条边的起始关键点的置信度是不是为0, 因为已经this_skel[kp['id'], 2] = kp['conf'], 所以第一次肯定不为0;但是如果第一次之后没有找到新的关键点的话,那么以后的循环都要continue
if this_skel[edge[0],2] == 0:
continue
# dir——edges 索引0-31
mid_idx = dir_edges.index(edge)
# mid_offsets shape=[h,w,32x2] 输出feature map的每个位置
offsets = mid_offsets[:,:,2*mid_idx:2*mid_idx+2]
# 计算当前给定的关键点基于grid的位置
from_kp = tuple(np.round(this_skel[edge[0],:2]).astype('int32'))
# 计算当前关键点的位置，加上，此位置针对该类型有向连接的预测的偏移x,y向量，得到的候选位置，
# 比如我们当前的关键点类型为左肘部，有向连接为（左肘，左手腕），那么根据该位置的mid-offset预测的左手腕的位置就知道了，但是这是根据mid-offset预测得到的位置，如果我们在hough score maps上也同样在该附近位置预测到了左手腕的位置，那么就说明mid-offset的预测也是合理的。
proposal = this_skel[edge[0],:2] + offsets[from_kp[1], from_kp[0], :]
# 所以接下的matches，是在优先级队列中找到候选的所有左手腕（假设）的关键点，并记录其在优先级队列中的位置i。（找到最佳匹配点后，需要把它从队列中pop出）
matches = [(i, keypoints[i]) for i in range(len(keypoints)) if keypoints[i]['id'] == edge[1]] # edge[1]表示有向线段的末端点（左手腕）
# 通过计算mid-offset预测出的有向线段末端点位置，与score maps 上该类型的位置的距离，我们可以得到很有可能的匹配关键点（<32）
matches = [match for match in matches if np.linalg.norm(proposal-match[1]['xy']) <= 32]
# 找不到匹配点的话，就队列中的下一个关键点
if len(matches) == 0:
continue
# 根据匹配到的该类型关键点与预测的距离进行排序，距离越小，排序靠前
matches.sort(key=lambda m: np.linalg.norm(m[1]['xy']-proposal))
# 排在最前面的关键点，即matches[0]，的坐标作为grid上的位置
to_kp = np.round(matches[0][1]['xy']).astype('int32')
# 记录其confidence
to_kp_conf = matches[0][1]['conf']
# 根据其在队列中的位置，将其pop出来
keypoints.pop(matches[0][0])
# 把该匹配到的点的位置记录到骨架该处有向线段的末端位置上
this_skel[edge[1],:2] = to_kp
this_skel[edge[1], 2] = to_kp_conf
# 此处我们进行path路径上的顺寻，进入下一个有向连接，
# 这里的path = iterative_bfs(skeleton_graph, kp['id']) 函数是个非常巧妙的扩散方式，
#它从骨架上的任意一点出发，按照固定的顺序散播到骨架上的所有16个有向连接上（上游点（父），下游点（子））。
#那么根据起始的任意一种人体关键点，这一个算法就可以在优先级队列中将很有可能属于该人体的所有关键点的候选点group到该人体上。
# 但是,如果考虑到有一种枢纽的关键点，没有找到合适的点，那么不完整的人体骨架将会产生，
# 但是在队列后面属于人体的关键点还会产生一个候选骨架，那么非极大值抑制skeleton就是必要的一项了
skeletons.append(this_skel)
return skeletons
## https://github.com/octiapp/KerasPersonLab/blob/master/post_proc.py
## https://github.com/senyang-ml/OKS-NMS
在G-RMI、PersonLab的基础上，引入了PAF和PIF 复合结构，实际上具备显式含义的向量场。
即在图像每个location的像素位置，寄托更多的复合含义，编码具有直观含义的向量
PIF针对每一种类型的关键点，PAF针对每一种关联肢体（两个有关part的连接连线）
对于COCO，有17个关键点，19个连接（论文默认设置）
PIF和PAF是训练Encoder网络用的监督标签，如何构造这两种标签，来指导监督Encoder网络训练，是本论文很关键的部分，后面的decoder 部分完全依赖于PIF和PAF的预测值。本文的PIF和PAF设计，可谓是将人工先验知识发挥到了极致！
PIF
PIF是个\(K\times H \times W \times 5\)的结构， K表示关键点的数量，COCO为17个
They are composed of a scalar component for confidence, a vector component that points to the closest body part of the particular type and another scalar component for the size of the joint. More formally, at every output location spread \(b\) (details in Section 3.4\()\) and a scale \(\sigma\) and can be written as
\[ \mathbf{p}^{i j}=\left\{p_{c}^{i j}, p_{x}^{i j}, p_{y}^{i j}, p_{b}^{i j}, p_{\sigma}^{i j}\right\} \]
因为作者主要针对小尺寸人体图片，那么得到的置信度图 confidence map 是非常粗糙的，为了进一步地提升confidence map 的定位精度，作者使用偏量位移maps 来提升confidence map 的分辨率，得到一个高分辨率的confidence map（这个高分辨率的置信图发挥着产生姿态种子点和评价候选点得分的作用），如下公式： \[
f(x, y)=\sum_{i j} p_{c}^{i j} \mathcal{N}\left(x, y | p_{x}^{i j}, p_{y}^{i j}, p_{\sigma}^{i j}\right)
\] 这个公式我发现，很大程度上借鉴了G-RMI中的上述公式。用一个未归一化的高斯核，以及可学习的范围因子\(\sigma\)来代替G-RMI中的双线性插值核以及归一化的分母，通过上述公式计算一个高分辨率的图（这里的高分辨率尺寸应该是原图尺寸，因为关键点的坐标标签真实值是基于原图的像素大小等级的）的响应值，我个人理解为是一种利用预测值的高斯上采样插值法（\(p_{x}^{i j}, p_{y}^{i j}\)是预测出的小尺寸置信图每个位置\((i,j)\)基于其自身grid位置\((i,j)\)的偏移量，\(p_{\sigma}^{i j}\)应该是高分辨图中每个位置的得分受到周围多大范围的预测值的影响，这部分应关注源码）。
这么做的缘故是，我认为是，想保证不论在何种尺寸（量化等级下）都能克服量化误差的影响，因为heatmap是基于grid的，离散的取值，而真实的位置是不基于grid，并且是连续的位置，我通过预测真实位置与grid位置的偏移、以及grid上的置信度，就能进而获知真实的精确位置。（我个人理解这样的好处就是，定位精度是float级别的，而不是int级别的，这个实际上在小尺寸的图像上是非常重要的一种策略。这种思想源自于G-RMI, 我认为这是一个解决量化误差问题的非常好的方式, 像SimpleBaseline,CPN运用取1/4偏移的方式,是一种人为的假设.）
PAF
PAF是个\(N\times H \times W \times 7\)的结构， N表示关联肢体的数量，默认为19，
作者使用的bottom-up的方法，必然要解决：关联检测的关键点的位置形成隶属的人体的这一问题，就必须用一定的表示手段和策略来实现。
作者提出了PAF，来将关键点连接一起形成姿态。
在输出的每个位置，PAFs预测一个置信度、两个分别指向关联一起的两个part的向量、两个宽度。用下面来表示： \[ \mathbf{a}^{i j}=\left\{a_{c}^{i j}, a_{x 1}^{i j}, a_{y 1}^{i j}, a_{b 1}^{i j}, a_{x 2}^{i j}, a_{y 2}^{i j}, a_{b 2}^{i j}\right\} \]
作者接下来说了这样一句话，
Both endpoints are localized with regressions that do not suffer from discretizations as they occur in grid- based methods. This helps to resolve joint locations of close-by persons precisely and to resolve them into distinct annotations。 我目前的理解是，两个端点定位的回归，不再受困于 grid-based方法中出现的离散化问题！这就帮助对于离得很近的关键点精确位置，并区分它们的标注。
在COCO数据集，一共有19个连接关联两种类型的关键点。算法在每个feature map的位置，构造PAFs成分时，采用了两步：
首先，找到关联的两个关键点中最近的那一个的位置，来决定其向量成分中的一个。
然后，groundtruth pose决定了另外一个向量成分。第二个点不必是最近的，也可以是很远的。
一开始我没有，怎么理解这么做的含义。后来意识到，这样就相当于，对于每一种类型的关联肢体，比如左肩膀和左屁股连接。对应的PAF中，每个位置都会优先确定理它最近的关键点的位置（考虑多个人体的情况下），然后指向另外一端的向量就自然得到了。
并且在训练的时候，向量成分所指向的parts对必须是相关联的，每个向量的x，y方向必须指向同一个关键点的。
Adaptive Regression Loss
定位偏差可能对于大尺寸人体来讲，是小的影响，但是对于小尺寸人体，这个偏差就会成为主要的问题。本研究通过引入尺度依赖到\(L_1 - type\)的loss函数里，
Greedy Decoding
通过PIF和PAF来得到poses。这个快速贪心的算法过程和PersonLab中的相似。
一个姿态由一个种子点(高分辨率PIF的最高响应位置)开始，一旦一个关键点的估计完成，决策就是最终不变的了。（贪心）
A new pose is seeded by PIF vectors with the highest values in the high resolution confidence map \(f(x, y)\) defined in equation \(1 .\) Starting from a seed, connections to other joints are added with the help of PAF fields. The algorithm is fast and greedy. Once a connection to a new joint has been made, this decision is final.
Multiple PAF associations can form connections between the current and the next joint. Given the loca- tion of a starting joint \(\vec{x},\) the scores \(s\) of PAF associations a are calculated with
\[ s(\mathbf{a}, \vec{x})=a_{c} \quad \exp \left(-\frac{\left\|\vec{x}-\vec{a}_{1}\right\|_{2}}{b_{1}}\right) f_{2}\left(a_{x 2}, a_{y 2}\right) \]
这个\(s(\mathbf{a},\vec{x})\)表示每个location属于part association的得分，得分越高，代表这个更有可能是part association区域部分那么,如果\(s(\mathbf{a},\vec{x})\)越大,那么就期望\(a_c\)越大,\(\left(-\frac{\left\|\vec{x}-\vec{a}_{1}\right\|_{2}}{b_{1}}\right)\)越大,\(\frac{\left\|\vec{x}-\vec{a}_{1}\right\|_{2}}{b_{1}}\)越小,那么就期望PAF某位置的\(\mathbf{a}\) 对应的\(\mathbf{a}=\left\{a_{c}^{i j}, a_{x 1}^{i j}, a_{y 1}^{i j}, a_{b 1}^{i j}, a_{x 2}^{i j}, a_{y 2}^{i j}, a_{b 2}^{i j}\right\}\)向量中, 其指向的端点1和当前种子点距离最近, 并且期望该位置指向的另外一个端点2的置信度响应高, 这些期望和该位置是属于这两个关键点(端点)连接肢体的期望是一致的. 一旦我们的初始种子点确立后,我们就可以根据预测的PAF找到其关联的肢体区域和另外一个关键点位置,作为下一次的寻找的种子点.然后,重复这个过程,直到该种子点对应的人体全部找到.(这实际运用了人体躯干的连通性的潜在知识). 作者提倒:
To confirm the proposed position of the new joint, we run reverse matching. This process is repeated until a full pose is obtained. We apply non-maximum suppression at the keypoint level as in [34]. The suppression radius is dynamic and based on the predicted scale component ofthe PIF field. We do not refine any fields neither during training nor test time.
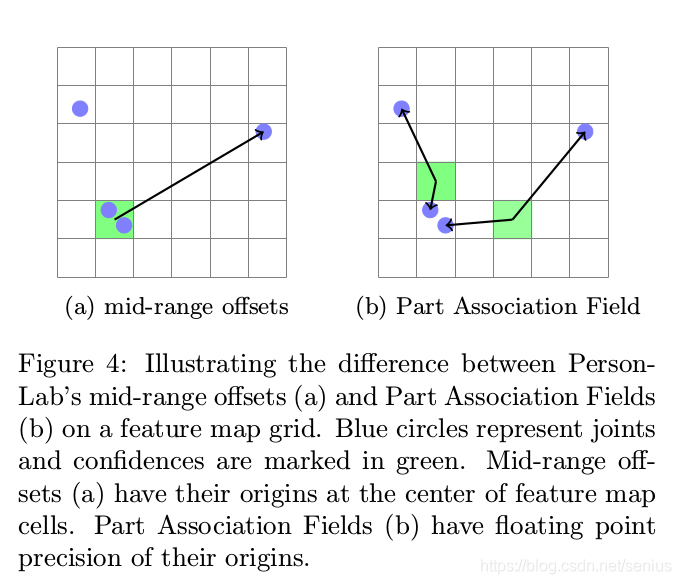
这个设计是巧妙的,因为我们在构造PAF的时候,请注意到,\((a_{x1},a_{y1})\) 是PAF输出map的某位置\(\mathbf{a}\)最近的关键点的位置（请看Figure 4b），以此来判断离该位置\(\mathbf{a}\)最近的关键点是不是\(\vec{x}\)。如果当前\(\vec{x}\)和\((a_{x1},a_{y1})\)的距离就可以作为当前位置是不是指向\(\vec{x}\)的判断,因为如果两点重合的话,距离为0,指数取值为最大值1. 并且该位置对应的另外一个端点的取值具有高响应, 那么这就意味着:
\(s(\mathbf{a}, \vec{x})\)的髙得分位置,很有可能处在指向\(\vec{x}\)端点的肢体关联部分的区域！
换句话说：
\(PIF\)是计算得到的高分辨率置信度图负责提供候选的关键点。\(s(\mathbf{a}, \vec{x})\)得分公式，利用\(PAF\)预测值计算在其输出feature map每一个位置的得分，来判断两种关键点之间的连接（如左肘部和左手腕），因为涉及到多人，（参考OpenPose，对于单个人体的单个肢体连接，只有一种连接是合理的），论文提到的To confirm the proposed position of the new joint, we run reverse matching，我认为就是来确定某人体的某个肢体连接的唯一性、合理性的手段，具体还是要看源码。
找到\((a_{x2},a_{y2})\)的位置(通过髙响应\(s(\mathbf{a}, \vec{x})\))的位置?还是通过PIF,PAF的预测值得到?这个目前有待考证，我在后面会阅读实现源码,继续更新博客)，高分辨率置信度图负责提供候选的关键点的位置。
那么，通过这样的一个贪心的快速算法, 我们根据初始的某个关键点就能同时确立多个人体位置,
思考
注：可以看出这一系列的论文（GRMI，PersonLab，Openpifpaf，part-based）相比与针对网络结构进行改进（SimpleBaseline，HRNET）的文章看，更加关注几何关系上的问题以及网络的输出表示形式。PersonLab，Openpifpaf面对更加有挑战性的BBOX-FREE方法，以及小尺寸，遮挡问题进行处理，确确实实能给人持续往下深入的启示和实际应用的潜力。针对改网络结构的文章，譬如HRNET，SEU-POSE，SIMPLEBASELINE，CPN等等，致力于寻找最有的卷积结构设计，而不怎么关注一些棘手的问题（用模型本身的能力来克服），为姿态估计行业引领性能的标准，并不断去探索神经网络结构可能发挥的极限。前者更适合去研究新方法，突破现有检测器约束的姿态估计框架，去挑战多人姿态估计的难题，后者给我们提供了，固有框架内可以进一步提升性能的很多实用的经验和技巧，让我们更加洞察神经网络的结构的特性，并充分利用神经网络结构设计的潜在能力。
哪个才能更好解决人体姿态估计问题的手段呢？