MetaAnchor - Learning to Detect Objects with Customized Anchors - 2018 NeurIPS 解读

NeuIPS 2018 > 原创博文转载请注明https://yangsenius.github.io/blog/MetaAnchor/

一般目标检测方法中的Anchors的生成是来自于人类的先验知识:\(b_i\in \mathcal{B} \ which \ is \ predefined \ by \ human\)（\(\mathcal{B}\)属于 \({prior}\) \(i\)代表网格或锚点），即

通过固定锚点，或者划分网格，生成一定形状和尺寸的Anchor Bboxes 来作为候选检测区域,提取对应位置的图像特征，

先验往往代表设计人员在构思最初的朴素想法，来源于直觉，并把这种直觉融合在设计者的实现过程与代码中。下面举两个例子。

在Faster Rcnn中

对输出的(W,H,d)维Conv map进行滑动遍历，每个滑窗输出一个特征向量WxH个d维的特征向量

根据根据感受野中心不变的原理，每个滑窗中心对应原图的anchor锚点或者说anchor bboxes的中心。

每个锚点映射到原图，实际上对应着来自3x3(3种特定的尺度x3个特定的形状)个的anchor boxes，我们认为这9个anchor bboxes经过特征提取得到的具有尺度不变性的特征向量，这些anchor bboxes意味着proposals。

然后作者使用先验规定：proposal与GTbbox iou大于某个阈值（0.7）认为是正样本，小于某个阈值（0.3）为负样本，其余的不参与训练！即给这些proposals做标签！

然后把这些正负样本送入RPN进行训练。

loss由regression和classification两个loss构成，即预测proposal的中心位置和宽高，以及proposal属于前景or背景

注意：这里的regression loss包含三个坐标：预测bbox、anchor bboxes、GT——bboxes,loss函数的目标是，缩小 [预测bbox与anchor bboxes相对偏移] 和[gt_bbox与anchor bboxes相对偏移]之间的差距！

经过RPN筛选后的Proposal的特征图的尺寸大小是不一致的，经过ROIPOOling得到特征维度一致的特征，使用与RPN共享卷积的Fast Rcnn进行进一步的分类和回归。

在yolo中

对任意输入尺寸的图像划分为\(s*s\)个网格

每个网格预测B个bbox的4个位置和1个置信度 - (confidence代表了所预测的box中含有object的置信度和这个box预测的有多准两重信息,object落在一个grid cell里，第一项取1，否则取0。第二项是预测的bounding box和实际的groundtruth之间的IoU值)

每个网格同时预测C个类的类别信息(每个网格属于的某类别的条件概率)

即对于一个输入图像，其输出的张量为 \(S*S*（B*5+C）\)

在这里，有必要说明，这里“Anchor先验”的含义，即：要把anchor的设计（位置、尺寸、类比）蕴含在anchor function的设计中，而不能成为一个独立的模块

作者总结了一个较为一般的形式：

\[\mathcal{F}_{b_i}(\mathbf{x};\theta_i)=\left(\mathcal{F}^{cls}_{b_i}(\mathbf{x};\theta^{cls}_i),\mathcal{F}^{reg}_{b_i}(\mathbf{x}; \theta^{reg}_i)\right)\]

判断： 1. 每个候选区域的与真实bbox（如果有）的相对位置 \(\mathcal{F}^{reg}_{b_i}(\mathord{\cdot})\) 2. 每个候选区域的类别置信概率 \(\mathcal{F}^{cls}_{b_i}(\mathord{\cdot})\)

本篇文章，作者使用的Anchor Function 是从先验的\(b_i\)动态生成的,通过如下函数：

\[\mathcal{F}_{b_i}=\mathcal{G}\left(b_i; w \right)(2)\]

\(\mathcal{G}(\mathord{\cdot})\) is called \({anchor \ function \ generator}\) which maps any bounding box prior \(b_i\) to the corresponding anchor function \(\mathcal{F}_{b_i}\); and \(w\) represents the parameters. Note that in MetaAnchor the prior set \(\mathcal{B}\) is not necessarily predefined; instead, it works as a manner -- during inference, users could specify any anchor boxes, generate the corresponding anchor functions and use the latter to predict object boxes.

上面是作者的原话，我觉得这个想法还是非常具有启发性的。我的理解是：

我们不是先盲目地生成大量的Anchor来判断是否抛弃，而是根据后面推理时的需要，在对应的位置生成特定的anchor boxes，然后生成anchor function来预测物体bbox，这样就避免了大量无关的候选框？这是我的理解，不知道对不对，接着读论文~

“default boxes” , “priors” or “grid cells” 经常作为一个默认的方法。很多任务需要你在设计achor的大小、尺寸、位置时需要小心谨慎，不同数据集之间的物体bbox分布也会影响anchor的选择，但是MetaAnchor的方法就不用考虑这个问题。
受到 Learning to learn、few shot learning 、transfer learning的启发：有时候，我们的权重预测不是通过模型本身来学习，而是通过另一个结构（模型）来取预测权重，比如（Learning to learn by gradient descent by gradient descent，hypernetworks等），作者还拿自己的方法和learning to segment everything 作了对比，作者的权重预测是为了生成anchor function。

仿佛，论文最关键的就是如何生成anchor function了，也就是这个函数了：

\[\mathcal{F}_{b_i}=\mathcal{G}\left(b_i; w \right)\]

下面详细讨论这个机制。

Anchor Function Generator

In MetaAnchor framework, \({anchor \ function}\) is dynamically generated from the customized box prior (or anchor box) \(b_i\) rather than fixed function associated with predefined anchor box. So, \({anchor \ function \ generator}\) \(\mathcal{G}(\mathord{\cdot})\) (see Equ.2), which maps \(b_i\) to the corresponding anchor function \(\mathcal{F}_{b_i}\), plays a key role in the framework.

作者强调了从\(b_i\)映射到anchor function \(\mathcal{F}_{b_i}\), 这种映射关系是因为\(b_i\)是带着一种随机性

In order to model \(\mathcal{G}(\mathord{\cdot})\) with neural work, inspired by HyperNetworks,Learning to segment everything, first we assume that for different \(b_i\) anchor functions \(\mathcal{F}_{b_i}\) share the same formulation \(\mathcal{F}(\mathord{\cdot})\) but have different parameters, which means:

\[\mathcal{F}_{b_i}(\mathbf{x}; \theta_i) = \mathcal{F}(\mathbf{x}; \theta_{b_i})\]

作者写这个公式，似乎想给出无论怎样选择\(b_i\) 的anchor function的一般形式。为什么这么做呢？下标的变换有什么意义吗？

我根据后面的内容，猜测：一般anchor function在设计时是要考虑 anchor\(b_i\)的预定义方式，也就是我们要根据不同的anchor先验，具体设计出相对应的anchor function。如果我们anchor function的设计能够独立于anchor\(b_i\)的预定义方式，让anchor\(b_i\)的设计变成一个函数的可学习的参数形式，那么就把问题转化为一般的超参数学习，或者Meta-learning 的方式。之前我研究Learning to learn by gradient descent by gradient descent，作者就是让人工干预设计的优化方式，变成了可以学习的参数，二者虽然面对的问题的不一样，但是都包含了一个共同的思想：

让人工设计的先验知识，转化成，可以通过另一个结构或模型学习的，参数形式：

\[人工先验知识 \rightarrow 可学习的参数形式\]

这个思想和我上一篇博客:learning to learn 所涉及的方法，在理念上不谋而合

接着看论文。

论文说道： > each anchor function is distinguished only by its parameters \(\theta_{b_i}\), anchor function generator could be formulated to predict \(\theta_{b_i}\) as follows:

\[\theta_{b_i} = \mathcal{G}(b_i; w) \\= \theta^* + \mathcal{R}(b_i; w)\]

就是说，每个anchor function 通过参数 \(\theta_{b_i}\) 来唯一确定(我的理解应该没错)，其中\(\theta^*\)代表共享参数（独立于\({b_i}\)，并且可以学习），残差项\(\mathcal{R}(b_i; w)\)依赖于 anchor bbox \({b_i}\)

然后\(\mathcal{R}(b_i; w)\)使用一个简单的两层全连接网络来表示：

\[\mathcal{R}(b_i, w) = \mathrm{W}_2 \sigma \left( \mathrm{W}_1 b_i \right)\]

作者还考虑把图像特征引入到参数 \(\theta_{b_i}\)的学习中：

\[\theta_{b_i} = \mathcal{G}(b_i; \mathbf{x}, w) \\ = \theta^* + \mathrm{W}_2 \sigma \left( \mathrm{W}_{11} b_i + \mathrm{W}_{12} r(\mathbf{x}) \right)\]

\(r(\mathord{\cdot})\) 用来给 \(\mathbf{x}\)降维;

以上就是论文的理论思想了！

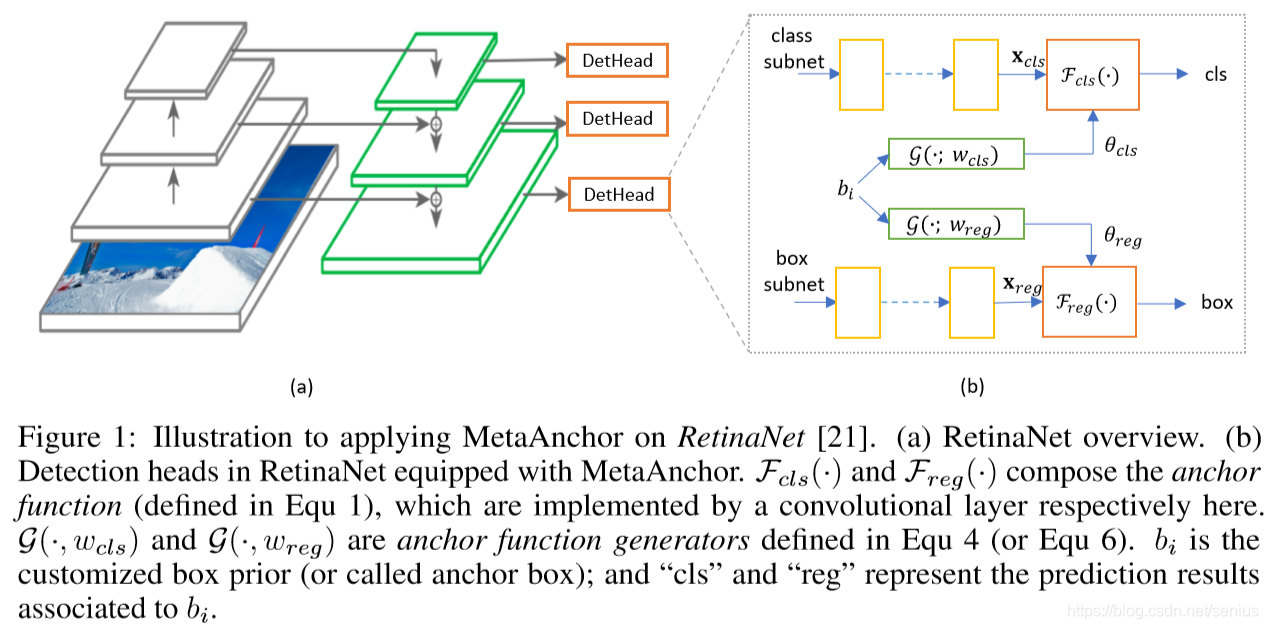
具体实施细节，结合RetinaNet代码，让我们来感受什么是“Prior”？什么是“Meta”

作者没有公布自己的源码是一件令人头疼的事情，这样就不知道，作者是如何把可学习的参数\(\theta_{b_i}\)如何融进anchor function，不过我后面会试图写一下。

作者说，这个方法更实用于one-stage的检测方法如 RetinaNet，yolo等，two-stage方法精度似乎受到第二阶段（anchor 不再发挥作用）的学习的影响更大。

作者主要说明了MetaAnchor在RetinaNet上的使用，先来看看什么是RetianNet，放上一段简介的代码

class RetinaNet(nn.Module):
    num_anchors = 9
    
    def __init__(self, num_classes=20):
        super(RetinaNet, self).__init__()
        self.fpn = FPN50()
        self.num_classes = num_classes
        self.reg_head = self._make_head(self.num_anchors*4)
        self.cls_head = self._make_head(self.num_anchors*self.num_classes)

    def forward(self, x):
        fms = self.fpn(x)
        reg_preds = []
        cls_preds = []
        for fm in fms:
            loc_pred = self.loc_head(fm)
            cls_pred = self.cls_head(fm)
            loc_pred = loc_pred.permute(0,2,3,1).contiguous().view(x.size(0),-1,4)                 # [N, 9*4,H,W] -> [N,H,W, 9*4] -> [N,H*W*9, 4]
            cls_pred = cls_pred.permute(0,2,3,1).contiguous().view(x.size(0),-1,self.num_classes)  # [N,9*20,H,W] -> [N,H,W,9*20] -> [N,H*W*9,20]
            loc_preds.append(loc_pred)
            cls_preds.append(cls_pred)
        return torch.cat(loc_preds,1), torch.cat(cls_preds,1)

    def _make_head(self, out_planes):
        layers = []
        for _ in range(4):
            layers.append(nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1))
            layers.append(nn.ReLU(True))
        layers.append(nn.Conv2d(256, out_planes, kernel_size=3, stride=1, padding=1))
return nn.Sequential(*layers)

注：以上代码来自于kuangliu/pytorch-retinanet

从以上代码

_make_head（self, out_planes)

函数中可以得知：我们必须把anchor的数量考虑并体现在RetinaNet最后一层卷积核的通道数量上。那么作为RetinaNET网络结构的这个卷积核部分，就包含了我先验的一种设计（Anchor类型数为9）。

这样做的弊端就是：假如我换了anchor的种类或数量，那么就要重新改变这个卷积核的设计，进而影响了网络的结构和参数学习，那么这就意味着我先前学习的对于9个Anchor的RetinaNet不再具有一般性，不再具备迁移学习的能力。

如果我想，换一种数据集bbox的分布，或者换一种先验anchor的选择方式，网络依旧能够使用的话，就必须将anchor的先验从原来的设计中剥离出来作为一个独立的结构，从而不影响整体结构的设计，并且可以根据需求自定义不同的anchor设计，这也就是这篇论文要解决的问题，并冠以“MetaAnchor”的称号，并使用了一个\(\mathcal{G}(b_i; w)\)的anchor function generator

在RetianNet 的原设计中，每个detection head模块最后一层，对于预定义的3x3中anchor bboxes ，anchor function中：

cls模块用3x3x80（类别）=720个通道卷积核，生成720维的预测向量
reg模块有3x3x4=36个通道卷积核，生成36维的预测向量

而在使用MetaAnchor后，就降成了：

cls模块有80（类别）=80个通道卷积核，生成80维的预测向量
reg模块有4个通道卷积核，生成4维的预测向量

这就就需要重新设计anchor function。根据自己定制（customized）的anchor bbox\({b_i}\)首先，应该考虑如何编码\({b_i}\)，它包含了位置、尺寸、类别信息，多亏了RetianNet的全卷积结构，位置坐标信息已经包含在Feature map 中，我们使用\(\mathcal{G}(\cdot)\)来预测类别，那么\({b_i}\)只需要包含尺寸信息：

\[b_i = \left(\log \frac{ah_i}{AH}, \log \frac{aw_i}{AW} \right)\]

在一个训练的mini-batch中，我们给定一个二维\(b_i\)的数值，分别经过两层的全连接网络\(\mathcal{G}(b_i; w_{cls})\)和\(\mathcal{G}(b_i; w_{reg})\)的映射，得到一个\(W_{cls}\)和\(W_{reg}\)维度的参数\(\theta_{cls,b_i}\)和\(\theta_{reg,b_i}\)

论文里面没有给出这个参数\(\theta_{cls,b_i}\)和\(\theta_{reg,b_i}\)如何写入到Loss function中，我根据作者思路猜测：

论文提到 \(\mathcal{G} \left(b_i, w\right)\) 是一个低秩的子空间

不过根据论文的权重预测的思想，这里的参数\(\theta_{cls,b_i}\)和\(\theta_{reg,b_i}\)应该在lossfunction中发挥权重的作用，在训练过程中，通过给定一个位置和尺度下的anchor bbox的输出和标签，乘以相应权重，来计算该anchor点对应的所有anchors总的loss:

import torch
import numpy as np
import torch.nn.functional as F

def Anchor_bbox_size(ah_i,aw_i,level):
        minimum_size = 20
        AH,AW = minimum_size * np.pow(2,level-1)
        b_i=(np.log(ah_i/AH),np.log(aw_i/AW))
        return b_i
        
def anchor_bbox_generator(b_i,level=1):
    '''b_i = (log(ah_i/AH),log(aw_i/AW))
       b_t = [N,2]     '''
    
    hidden_dim = 5
    theta_dim = 10
    theta_standard =torch.randn(theta_dim)
    
    ## two -layer
    Residual_theta =F.linear( F.relu (F.linear(bi,(2,hidden_dim))) , (hidden_dim,theta_dim ) )
    
    theta_b_i = theta_standard + Residual_theta
    
    reutrn theta_b_i

class RetinaNet(nn.Module):
    
    def __init__(self, num_classes=20):
        super(RetinaNet, self).__init__()
        self.fpn = FPN50()
        self.num_classes = num_classes
        self.reg_head = self._make_head(4)
        self.cls_head = self._make_head(self.num_classes)

    def forward(self, x):
        fms = self.fpn(x)
        reg_preds = []
        cls_preds = []
        for fm in fms:
            loc_pred = self.loc_head(fm)
            cls_pred = self.cls_head(fm)
            loc_pred = loc_pred.permute(0,2,3,1).contiguous().view(x.size(0),-1,4)            # [N, 4,H,W] -> [N,H,W, 4] -> [N,H*W, 4]
            cls_pred = cls_pred.permute(0,2,3,1).contiguous().view(x.size(0),-1,self.num_classes)  # [N,20,H,W] -> [N,H,W,20] -> [N,H*W,20]
            loc_preds.append(loc_pred)
            cls_preds.append(cls_pred)
        return torch.cat(loc_preds,1), torch.cat(cls_preds,1)

    def _make_head(self, out_planes):
        layers = []
        for _ in range(4):
            layers.append(nn.Conv2d(256, 256, kernel_size=3, stride=1, padding=1))
            layers.append(nn.ReLU(True))
        layers.append(nn.Conv2d(256, out_planes, kernel_size=3, stride=1, padding=1))
return nn.Sequential(*layers)

def focal_loss_meta(bi,cls_pred,cls_label,reg_pred,reg_label):
    '''
    bi = [N,2]
    cls_pred = [N,20]
    cls_label = [N,]
    reg_pred = [N,4]
    reg_label = [N,4]
    
    '''
    
   
    alpha = 0.25
    gamma = 2
    num_classes = 20
    
    t = torch.eye（num_classes+1）(cls_label, ）  # [N,21] 20+背景 
    # t is one-hot vector
    t = t[:,1:]  # 去掉 background 【N，20】 
   

    p = F.logsigmoid(cls_pred)
    pt = p*t + (1-p)*(1-t)         # pt = p if t > 0 else 1-p
    m = alpha*t + (1-alpha)*(1-t)   
    m = m * (1-pt).pow(gamma)   # focal loss 系数 解决样本不平衡
    
    weight = anchor_bbox_generator(bi,) # [N,W] W维的θ参数，该怎么用？ 还是说这里W=1？？
    
    cls_loss = F.binary_cross_entropy_with_logits(x, t, m, size_average=False)

以上代码仅代表个人对论文的局限理解

因为看不到论文的代码，目前我理解最模糊的就是这个θ参数如何与loss function相结合的地方了，还请网友多多交流，欢迎发表更多的见解~

以上基本就介绍了是论文最主要的想法：

MetaAnchor对于anchor的设定和bbox的分布更加鲁棒
MetaAnchor可以缩减不同数据集bbox分布的差异的影响，即更具迁移学习的能力！

论文的更多的实验细节，我会继续阅读并更新博客~

=========================================

上次博客中说道，我理解最模糊的就是这个θ参数如何与ancnhor 的 loss function相结合的地方了

我重新阅读了论文，作者提到了权重预测的主要受到HyperNetworks的启发,然后我找来这篇论文，刚读完摘要，就恍然大悟理解了MetaAnchor里预测权重的思想，即这个θ参数的内涵，\(\theta_{b_i}\) 即 \(\mathcal{F}_{csl}\left(\cdot\right)\) 和 \(\mathcal{F}_{reg}\left(\cdot\right)\) 的中的参数，在RetinaNet中代表了最后一层卷积核的参数！

原来我在这个点上理解困难的原因是头脑中少了“HyperNetworks”的先验！

看来很多情况下，我们理解的困难源于：少了某些“先验知识”

HyperNetwork (ICLR2017)

HyperNetwork是什么呢，简言之：

用一个网络(A-HyperNetwork)生成另外另一个网络(B-主体网络)的权重

听起来很神奇，因为我们一般对于网络B的学习，通常经过梯度下降法产生梯度来更新参数。而这个工作可以直接用另一个网络的输出来预测。这样做的好处就是，我们可以将巨大参数量的权重学习，转换为一个小网络的参数学习，并可以通过端到端梯度优化的方法学习！

这篇论文分析了LSTM和CNN使用HyperNetwork的方法和效果，结合我们主要论述的MetaAnchor，我来简要介绍一下Static HyperNetwork在CNN中的应用

通过一个两层全连接的小网络，用一个layer embedding来预测（表征）CNN的卷积核参数值

对于一个深度的卷积神经网络，其参数主要由卷积核构成

每个卷积核有 \(N_{in} \times N_{out}\) 个滤波器每个滤波器有 \(f_{size} \times f_{size}\).

假设这些参数存在一个矩阵 \(K^j \in \mathbb{R}^{N_{in}f_{size} \times N_{out}f_{size}}\) for each layer \(j = 1,..,D\), 其中 \(D\) 是卷积网络的深度

对于每一层 \(j\), hypernetwork 接受一个 a layer embedding \(z^j \in \mathbb{R}^{N_{z}}\) 作为输入，并预测 \(K^j\), 可以写成:

\[ {K^j} = g( {z^j} ),\forall j = 1,..., D\]

\[{K} \in \mathbb{R}^{ N_{in}f_{size} \times N_{out}f_{size}}, {z} \in \mathbb{R}^{N_z}\]

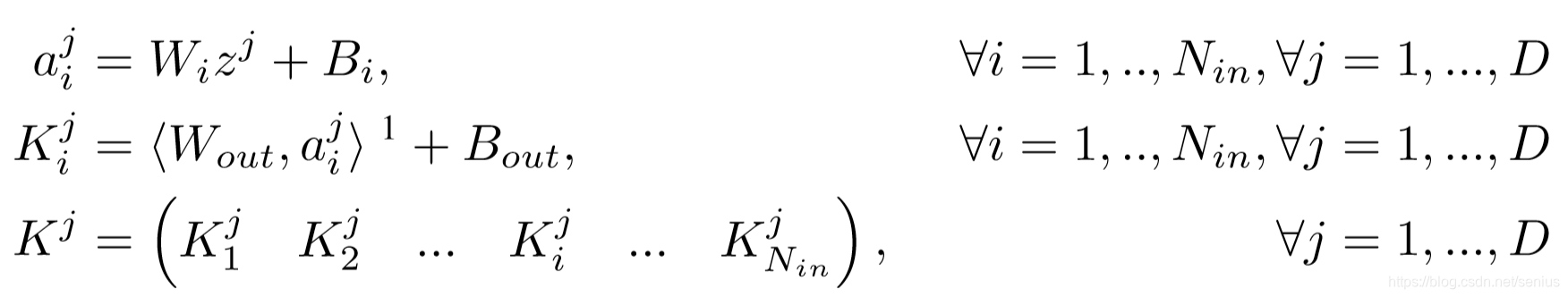
公式中，所有可学习的参数 \(W_i\), \(B_i\), \(W_{out}\), \(B_{out}\) 对于所有 \(z^{j}\)共享

在推理时, 模型仅仅将学习到的 the layer embeddings \(z^j\) 来生成第 \(j\) 层的卷积核权重参数

这就将可学习的参数量改变了:

\[D \times N_{in} \times f_{size} \times N_{out}\times f_{size}\]

\[\rightarrow\]

\[N_{z}\times D + d\times (N_z + 1)\times N_i + f_{size}\times N_{out}\times f_{size}\times (d+1)\]

应用到MetaAnchor中：\(\theta_{b_i}\)即RetinaNet的最后一层卷积核的参数

即，我们用自定义anchor设计\({b_i}\)成二维向量，作为“layer embedding”，输入两层的网络，预测了RetinaNet的最后一层卷积核参数的残差，这样就降低了原RetinaNet的卷积核滤波器的数量，就像之前提到的。

～～2019年6月25日更～～ 最后，可能还需要再次提到关于\(\theta^*\) 和\(\mathcal{R}(b_i; w)\)这两项的理解：

公式提到： \[\theta_{b_i} = \mathcal{G}(b_i; w) \\= \theta^* + \mathcal{R}(b_i; w)\]

我们想要学习的是\(\theta_{b_i}\) ，它有两部分构成：\(\theta^*\) 和\(\mathcal{R}(b_i; w)\)，当进行学习的时候，梯度流到\(\theta_{b_i}\) 节点，会产生\(\theta^*\) 和\(\mathcal{R}(b_i; w)\)的梯度：\(\nabla\theta^*\) 和\(\nabla\mathcal{R}(b_i; w)\), 而\(\nabla\theta^*\)可以直接用来更新\(\theta^*\) ，但\(\nabla\mathcal{R}(b_i; w)\)进一步通过HyperNetwork网络流到其参数\(\nabla w\)上，然后更新HyperNetwork的参数\(w\)。以上是进一步的分析了，如果有问题欢迎提出～